 por SCHOOLGIRL+T » Qua Nov 07, 2012 09:08
por SCHOOLGIRL+T » Qua Nov 07, 2012 09:08
O gráfico da função f(x) = x² + ax + a + 1 tem um valo mínimo igual a zero. O produto dos possíveis valores de a é:
a) -1
b) -2
c) -3
d) -4
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qua Nov 07, 2012 11:48
por young_jedi » Qua Nov 07, 2012 11:48
se seu valor minimo é igual a zero isso significa que este é o valor do vertice da função, que é calculdo por
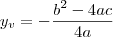
substituindo os valores da equação da curva: (Obs: repare que este a da formula acima não é o mesmo a da sua equação)
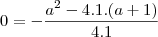
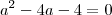
resolvendo por baskara voce encontra os valore de a e fazendo o produto voce encontra o resultado
mais repare que não é necessario, pois numa equação do segundo grau sabemos que o termo independente que nesse caso é -4 é igual ao porduto das raizes(que nesse caso são os dois valores de a) portanto a resposta é igual a -4
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9024 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2531 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 1936 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2016 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
-
- Função Quadratica
 por guijermous » Sáb Abr 10, 2010 10:02
por guijermous » Sáb Abr 10, 2010 10:02
- 4 Respostas
- 7897 Exibições
- Última mensagem por Molina

Sáb Abr 10, 2010 16:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



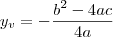
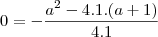
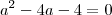


 .
.



