Saudações caros estudantes!
Vou começar definindo 2 acepções para o termo função:
1) no sentido geral: conjunto de operações executadas por algo ou alguém.
2) no sentido matemático: uma grandeza y variando por causa da variação duma grandeza x
Pois bem, é certo afirmar que a Integração ou a Derivação duma função genérica f(x) é uma função no 2º sentido acima citado por mim, o matemático?
Creio que sim, porque:
seja y uma função f(x) qualquer
der(y) = y'
int(y) = Y
aplicamos a derivada e a integral numa função genérica como aplicamos a função seno e cosseno num ângulo qualquer... não é verdade!?
PS.: sendo y?¹ uma função inversa genérica, a melhor notação (sem colchetes) para denotar a sua derivada seria: y?¹' ou y'?¹ ?
Obg,


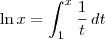 , para tomar um exemplo simples.
, para tomar um exemplo simples.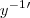 .
.


 .
.
 :
: