 por umbrorz » Qui Mai 10, 2012 15:23
por umbrorz » Qui Mai 10, 2012 15:23
Fala pessoal, minha dúvida é aquela resenha que rolava na internet.
Quanto é o resultado dessa expressão:
6/2(1+2)
É 9 ou 1. :x
VLW !
-
umbrorz
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Abr 15, 2012 00:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ADMINISTRAÇÃO
- Andamento: cursando
 por DanielFerreira » Qui Mai 10, 2012 21:59
por DanielFerreira » Qui Mai 10, 2012 21:59
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizAquino » Sex Mai 11, 2012 08:06
por LuizAquino » Sex Mai 11, 2012 08:06
umbrorz escreveu:Fala pessoal, minha dúvida é aquela resenha que rolava na internet.
Quanto é o resultado dessa expressão:
6/2(1+2)
É 9 ou 1. :x
A notação dada por "6/2(1+2)" é equivalente a notação
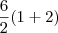
.
Se o objetivo fosse a notação
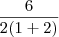
, então a forma correta equivalente seria 6/[2(1 + 2)].
Note a importância do uso adequado dos delimitadores (isto é, "( )", "[ ]" e "{ }").
Sendo assim, o correto é afirmar que 6/2(1+2) = 9.
Por outro lado, temos que 6/[2(1+2)] = 1.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Estou em duvida em como fazer essa expressão númerica
por GabrieleSales » Qui Nov 21, 2013 03:29
- 1 Respostas
- 2287 Exibições
- Última mensagem por DanielFerreira

Ter Fev 18, 2014 10:45
Aritmética
-
- Expressão numérica
por thadeu » Qua Nov 18, 2009 16:12
- 1 Respostas
- 2688 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 18:44
Álgebra Elementar
-
- Expressão numerica
por karenblond » Ter Mai 15, 2012 23:55
- 6 Respostas
- 4027 Exibições
- Última mensagem por Cleyson007

Ter Mai 22, 2012 19:50
Funções
-
- [Expressao Numerica]
 por lokido_ » Dom Out 11, 2015 03:34
por lokido_ » Dom Out 11, 2015 03:34
- 4 Respostas
- 2829 Exibições
- Última mensagem por adauto martins

Qui Out 15, 2015 19:14
Funções
-
- Matemática Básica - Expressão Numérica
por carolinabandeira » Sáb Ago 25, 2018 20:42
- 3 Respostas
- 3255 Exibições
- Última mensagem por Gebe

Dom Ago 26, 2018 08:42
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



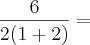
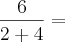
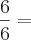

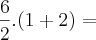

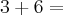
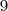

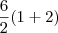 .
.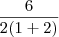 , então a forma correta equivalente seria 6/[2(1 + 2)].
, então a forma correta equivalente seria 6/[2(1 + 2)].