 por Aquamarine » Seg Fev 06, 2012 19:24
por Aquamarine » Seg Fev 06, 2012 19:24
Para todo x Pertencente ]?/2 ?/2] (tg x² + 1) . (sen x² –1) é –1.
Pelo gabarito a afirmação é correta
Mas eu fiz e deu diferente
(tg x² + 1) . (sen x² –1)
Pela relação derivada
(tg x² + 1)= secx²
secx² . senx²-1 =
1/cosx² . senx ² =
senx²-1/cosx²
que equivale a tgx²-1
Se alguem alguem souber a
aagradeço
-
Aquamarine
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Fev 06, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por ant_dii » Seg Fev 06, 2012 21:15
por ant_dii » Seg Fev 06, 2012 21:15
Bom, primeiramente você deve se atentar ao fórum correto para sua dúvida... O que você esta postando é sobre função trigonométrica. Mas já que aqui estamos vamos lá...
Aquamarine escreveu:Para todo x Pertencente ]?/2 ?/2] (tg x² + 1) . (sen x² –1) é –1.
Bom você quer dizer que
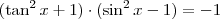
.
Sim isto é verdade, veja que, como você colocou
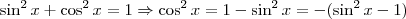
e
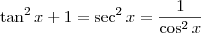
Assim
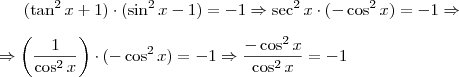
...
Feito??
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função afim] Determinar a função afim
por Apprentice » Dom Set 30, 2012 21:49
- 4 Respostas
- 3087 Exibições
- Última mensagem por Apprentice

Seg Out 01, 2012 12:19
Funções
-
- funçao afim
por maiara amaral » Dom Mai 11, 2008 18:08
- 2 Respostas
- 4763 Exibições
- Última mensagem por Kabarosk

Sex Mai 29, 2015 01:45
Pedidos
-
- Funçao Afim
por thais silva » Qua Mai 19, 2010 17:30
- 3 Respostas
- 2870 Exibições
- Última mensagem por MarceloFantini

Seg Jul 12, 2010 22:04
Funções
-
- funçao afim
por emilly » Ter Ago 17, 2010 20:40
- 6 Respostas
- 7051 Exibições
- Última mensagem por emilly

Qui Ago 19, 2010 18:32
Funções
-
- Função Afim
por Kelvin Brayan » Ter Mai 31, 2011 01:59
- 1 Respostas
- 2861 Exibições
- Última mensagem por Kelvin Brayan

Ter Jun 07, 2011 16:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


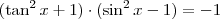 .
.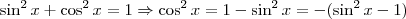
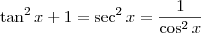
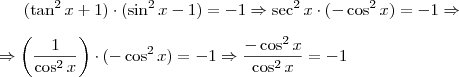

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)