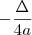essa funçao eh uma funçao quadratica... por isso o grafico dela tem a forma
duma parabola
ela pode ser escrita como

, onde a = 1, b = 4 e c = 5.
a partir desses numeros a gente pode saber detalhes sobre a parabola pra desenha-la
porque a > 0, a parabola tem a concavidade voltada pra cima.
o(s) ponto(s) onde y = 0 eh (sao) as raizes da equaçao

.
Esse(s) eh(sao) os pontos onde o grafico da funçao passa pelo eixo x. vamos procurar as raizes:
as raizes
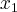
e

sao dadas pela formula:
![{x}_{1} = \frac{-b + \sqrt[]{\Delta}}{2a} {x}_{1} = \frac{-b + \sqrt[]{\Delta}}{2a}](/latexrender/pictures/1c675ba64b671ce1ed48218085cc8b49.png)
e
![{x}_{2} = \frac{-b - \sqrt[]{\Delta}}{2a} {x}_{2} = \frac{-b - \sqrt[]{\Delta}}{2a}](/latexrender/pictures/656fff597f562bf916316ed161c4561e.png)
onde

entao vamos calcula o \Delta



como teriamos q axar a raiz quadrada de -4 e numeros negativos nao tem raiz quadrada

isso significa que a parabola nao corta o eixo x...
o ponto onde ela corta o eixo Y eh o ponto onde X eh zero... esse eh facil eh soh calcular f(0):

a funçao corta o eixo y em (0, 5)
agora, o vertice da parabola eh dado pela formula
Vx =

Vy =

ou
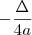
nesse nosso caso:
Vx =

e
Vy =

assim o vertice eh o ponto (-2, 1)
agora sabendo a esses dados importantes dela vc coloca mais uns outros pontos escolhendo valores pra x e pronto

ops... enquanto eu escrevia alguem respondeu hehe... disculpa ae




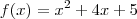
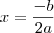
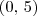

 , onde a = 1, b = 4 e c = 5.
, onde a = 1, b = 4 e c = 5. .
.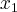 e
e  sao dadas pela formula:
sao dadas pela formula:![{x}_{1} = \frac{-b + \sqrt[]{\Delta}}{2a} {x}_{1} = \frac{-b + \sqrt[]{\Delta}}{2a}](/latexrender/pictures/1c675ba64b671ce1ed48218085cc8b49.png)
![{x}_{2} = \frac{-b - \sqrt[]{\Delta}}{2a} {x}_{2} = \frac{-b - \sqrt[]{\Delta}}{2a}](/latexrender/pictures/656fff597f562bf916316ed161c4561e.png)







 ou
ou