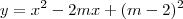, sendo m um número inteiro não negativo, não intersepta o eixo x em nenhum ponto. Então o valor mínimo que essa função assume é: A-( ) 1
B-( )4
C-( )0
D-( )1/2
Eu sei que delta é maior ou igual a zero. Mas não sei resolver
por maria cleide » Seg Ago 29, 2011 22:39
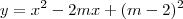, sendo m um número inteiro não negativo, não intersepta o eixo x em nenhum ponto. Então o valor mínimo que essa função assume é: 
por MarceloFantini » Ter Ago 30, 2011 09:05
não intercepta o eixo x em nenhum ponto, não há raízes, e portanto o discriminante é menor que zero. O seu valor mínimo será atingido no vértice da parábola, visto que ela tem "boca para cima". Para encontrar, use que a abscissa do vértice é dada por 
, e coloque isso na função para encontrar seu valor.
por maria cleide » Ter Ago 30, 2011 11:30
achei 
e não consegui prosseguir, por favor me explique como continuo.por MarceloFantini » Ter Ago 30, 2011 11:45
. Agora, note que como delta é negativo, temos 
e por m ser inteiro não-negativo, 
. O único valor que satisfaz é 
, e logo 
.por maria cleide » Ter Ago 30, 2011 22:34
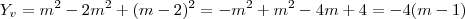, mas de onde tirou esses valores sendo que 
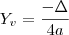que dá 
?por MarceloFantini » Qua Ago 31, 2011 08:51
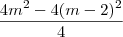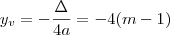. Faça as contas e verá que é a mesma coisa. Tome cuidado pois 
.
por guijermous » Sáb Abr 10, 2010 10:02
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)