[hipérbole / cônica] Funções

[Cleyson007]

Olá Fabio Sousa, boa noite!!!

Estou me dedicando ao estudo das "Funções", e, inclusive estou com algumas que gostaria de dicutir aqui no fórum, mas, vou precisar de fazer o diagrama delas. Gostaria de saber se há como fazê-lo pelo editor de fórmulas (LaTeX)!!!

Aproveitando a oportunidade... Gostaria que me desse uma dica quanto ao raciocínio da questão que segue.

A questão é a seguinte ---> Explicitar o domínio da função: .

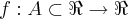a)

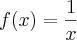
Estive pensando sobre a questão ---> No meu modo de pensar, só não pode ser , ou seja, deve ser .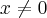

Agora , realmente pode assumir qualquer outro valor real?

Por favor me ajude!

Até mais

[admin]

Olá Cleyson, boa tarde, desculpe a ausência.

Para representar gráficos no fórum você precisa enviá-los como imagens.
Antes, as imagens precisam ser geradas localmente em seu computador através de alguma ferramenta.

Neste tópico há um comentário sobre os programas que você pode utilizar:
http://www.ajudamatematica.com/viewtopic.php?f=118&t=289&p=741#p741

Sobre a sua dúvida, sim, o domínio desta função apenas não contém o zero, pode ser qualquer outro valor real.

Esta é uma hipérbole, uma representante das cônicas (uma seção de cones):

Cada cônica possui propriedades particulares.
A hipérbole é um conjunto de pontos para os quais a diferença das distâncias a dois pontos fixos é constante.
Estes "pontos fixos" são chamados de focos.

Sobre o esboço de gráficos:
http://www.ajudamatematica.com/viewtopic.php?f=72&t=150&p=299#p299

A idéia comentada neste tópico é sobre partir de uma função conhecida mais simples da classe e representar, em etapas, as variações, por exemplo: translações horizontais e verticais (envolvendo alterações das raízes, quando existirem), "esticar" e "encolher" a função etc.

Bons estudos!