Quais dos seguintes subconjuntos
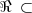RxR são relações de equivalência sobre R?a)
= {
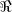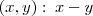é um inteiro par};b)
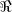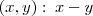= { é racional};c)
= {
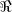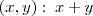é um inteiro par};d)
= {
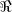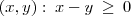é um inteiro par};No item a: acho que é equivalente,a justificativa que dou é:
por exemplo (5,5)
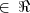; (1,3) e (3,1) 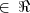, assim como também (1,1) 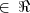, então é reflexiva, simétrica e transitiva;no item b: bem se x - y é racional as possiblidades são ampliadas pois o
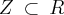, por isso é equivalente, será que esta seria uma justificativa plausível? 
no item C:
pelas mesmas razões do item a) são exemplos: (5,5)
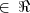; (1,3) e (3,1) 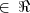, assim como também (1,1) 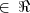, então é reflexiva, simétrica e transitiva;No item d) não é equivalente:
pois, por exemplo (5,3)
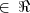; (3,5)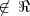 
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.