Como posso demonstrar que

Obrigado
Abraços!



 ou
ou  .
.

 então extraindo a raiz quadrada de ambos os membros terás que
então extraindo a raiz quadrada de ambos os membros terás que  .
.
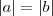 , e que então temos dois casos:
, e que então temos dois casos:  ou
ou  . Só podemos afirmar que é o primeiro se for dito que
. Só podemos afirmar que é o primeiro se for dito que 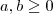 .
.

 , então
, então  ou
ou 
 , então são iguais, se são iguais, então
, então são iguais, se são iguais, então  = 0
= 0 (que é zero) também é igual a
(que é zero) também é igual a  então:
então: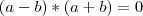 e se isso aí é zero então:
e se isso aí é zero então:  ou
ou 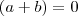
 temos:
temos:  e
e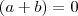 temos:
temos: 
 , mas que na verdade tenho que provar as duas hipóteses:
, mas que na verdade tenho que provar as duas hipóteses:  e
e 


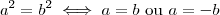 ?
?

 e para isso eu caio em duas hipóteses (está correto o termo ?):
e para isso eu caio em duas hipóteses (está correto o termo ?):  e
e  então.. provar essas duas últimas... que foi o que fiz..
então.. provar essas duas últimas... que foi o que fiz.. 
 , isso é sua hipótese. Se você chegou que
, isso é sua hipótese. Se você chegou que  ou
ou  , isso é sua tese.
, isso é sua tese.


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante