(ITA) Sejam A um conjunto com 8 elementos e B um conjunto tal que A U B contenha 12 elementos. Então, o número de elementos de P(B-A) U P(conjunto vazio) é igual a:
(a) 8
(b)16
(c) 20
(d) 17
(e) 9
única coisa que sei é que A U B = n(a) + n(b) -
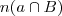, ai complica ,sei também que o conjunto das partes é
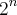onde n é o número de elementos do conjunto .Mais a maior dúvida que tenho e gostaria que se possível me exclaressem à principio ela é se A U B = 12
e A = 8 B - A = 4 eu posso afirmar isso ?
o resultado é B
e tem outra louca :
Denotemos por n(X) o número de elementos
de um conjunto finito X. Sejam A, B e C conjuntos
tais que n(A U B) = 8, n(A U C) = 9,
n(B U C) = 10, n(A U B U C) = 11 e
n(A ? B ? C) = 2. Então, n(A) + n(B) + n(C)
é igual a :
a) 11. b) 14. c) 15. d) 18. e) 25.
Temos:
n(A U B) = 8 <=> n(A) + n(B) ? n(A ? B) = 8 <=>
n(A ? B) = n(A) + n(B) ? 8
Da mesma forma,
n(A U C) = 9 <=> n(A ? C) = n(A) + n(C) ? 9 e
n(B U C) = 10 <=> n(B ? C) = n(B) + n(C) ? 10.
Como n(A U B U C) = 11 e n(A ? B ? C) = 2,
concluímos que:
n(A U B U C) = n(A) + n(B) + n(C) ? n(A ? B) ? n(A ? C) ? n(B ? C) + n(A ? B ? C) eu li esta resolução em outro site da internet isto é uma fórmula de conjuntoss ?
por