"Prove que
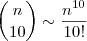 ",
",mas não me recordo o que significa este "til" entre as duas equações.
E quanto ao logaritmo neperiano: o que é o
 , não o valor, mas sim o que ele significa, como chegamos a ele, e também, como se "resolve" algo do tipo
, não o valor, mas sim o que ele significa, como chegamos a ele, e também, como se "resolve" algo do tipo 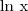 .
.Alguém poderia me ajudar com estas dúvidas?
Desde já, agradeço muito.
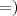

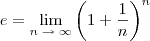

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)