Gente, voltei a estudar a algum tempo, e achei esse fórum, oque eu mais precisava, porém, estou com dificuldade pra resolver essa inequação. Procurei como resolver essa inequação, porém nada me esclareceu a dúvida
Resolva as inequações a seguir, no universo dos números reais (U=R)
1º (x - 3)^4 > 0
2º (x - 3)^4 < 0
Por favor, me ajudem com ela, me explicando como resolver ela.
Obrigado
Edit: Tentei de tudo, porém, não consigo entender por que a resposta do livro, li tudo sobre inequações, mas não consegui ainda intender por que a resposta da primeira inequação da 3, e a segunda da zero


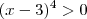

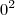 .
.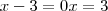 . Significa que neste valor essa expressão é igual a zero (e não maior do que zero). Então não nos importa.
. Significa que neste valor essa expressão é igual a zero (e não maior do que zero). Então não nos importa.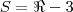

 - {3}.
- {3}.

 .
.
 :
: