Olá José Mário. Vamos tentar resolver esse problema.
As equações (todas elas) são como balanças de dois pratos: para manter o equilíbrio, tudo que se fizer em um dos pratos deve-se repetir a mesma operação no outro.
Ao usar as equações, eu recomendo que você utilize somo subtração e multiplicação. Divisão, exponenciação e radiciação contém alguns detalhes mais sutis. Essa equação mesmo apresenta uma condição de existência: o denominador deve ser diferente de zero. Sendo assim,
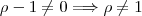
. Vamos aos cálculos:
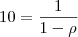
Admitindo que
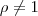
vamos multiplicar ambos os membros por

:
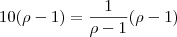
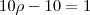
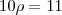
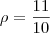
Como
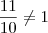
então essa solução é válida. Espero ter ajudado. Qualquer erro, por favor, AVISEM!!!
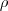 dessa equação:
dessa equação:

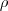 dessa equação:
dessa equação:




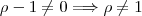 . Vamos aos cálculos:
. Vamos aos cálculos: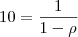
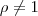 vamos multiplicar ambos os membros por
vamos multiplicar ambos os membros por  :
: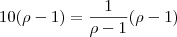
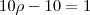
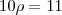
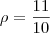
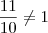 então essa solução é válida. Espero ter ajudado. Qualquer erro, por favor, AVISEM!!!
então essa solução é válida. Espero ter ajudado. Qualquer erro, por favor, AVISEM!!!