Sabendo-se que 2,777... = 2 +
+ 
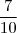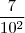+ ...e 0,111... =
+ 
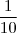... conclui-se que 
+ 
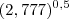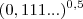é igual a:(A) 1,444...
(B) 2
(C) 2,888...
(D) 3
Eu tentei a achar a fração motriz de 2,777... e 0,111....
Eu encontrei, respectivament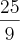e,
e 
.Eu manti o expoente inalterado:
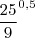e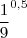 
Aí eu tranformei esse 0,5 em fração
e fiz a raiz quadrada. Aí q empatei e tentei transformar 
em 
Isso é possível? Pq assim consegui resolver, mas nao foi certo. Obrigado pela atenção de todos
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.