 por Ze Birosca » Qua Fev 04, 2015 18:55
por Ze Birosca » Qua Fev 04, 2015 18:55
Sendo:
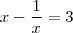
dertemine o valor de
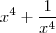
o gabarito marca 119, mas eu não faço a minima de ideia de como chegar a esse resultado.
A primeira coisa que eu pensei em fazer foi
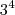
, mas acho que estou errado.
-
Ze Birosca
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Fev 04, 2015 18:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Fev 04, 2015 20:06
por Russman » Qua Fev 04, 2015 20:06
Tome

. Agora, elevemos ao quadrado.
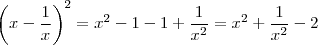
Portanto,
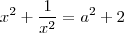
.
Repitamos o processo.
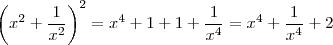
Portanto,
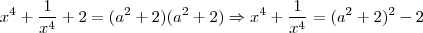
.
Fazendo a=3 você obtém 119.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Ze Birosca » Qua Fev 04, 2015 20:49
por Ze Birosca » Qua Fev 04, 2015 20:49
obrigado Russman, mas não estou conseguindo enteder essa parte aqui:
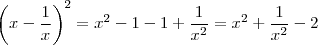
de onde vêm esse 1-1?
se eu fizesse:
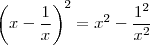
eu estaria errando?
-
Ze Birosca
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Fev 04, 2015 18:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Fev 04, 2015 20:58
por Russman » Qua Fev 04, 2015 20:58
Certamente.
Lembre-se que
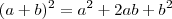
para todo a e b reais.
É fácil verificar a validade desta identidade. Tome, por exemplo, a=2 e b=3. Assim,
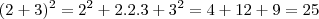
como devia ser, já que sabemos que
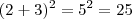
.
Agora, tome
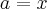
e
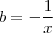
.
Assim, seguindo a identidade,
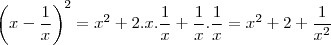
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Ze Birosca » Qua Fev 04, 2015 21:56
por Ze Birosca » Qua Fev 04, 2015 21:56
Ah, agora entendi.
fiz agora com o a = 3 e cheguei ao resultado.
Obrigado.
-
Ze Birosca
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Fev 04, 2015 18:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Amigos não estou conseguindo resolver o exercicio...
por Catriane Moreira » Seg Set 06, 2010 21:56
- 1 Respostas
- 1677 Exibições
- Última mensagem por Cleyson007

Seg Set 06, 2010 23:15
Sistemas de Equações
-
- Não estou conseguindo resolver
por Douglas Canto » Qua Nov 03, 2010 13:05
- 0 Respostas
- 4173 Exibições
- Última mensagem por Douglas Canto

Qua Nov 03, 2010 13:05
Estatística
-
- Amigos e amigas eu não estou conseguindo resolver
por Catriane Moreira » Seg Nov 08, 2010 20:23
- 1 Respostas
- 1555 Exibições
- Última mensagem por esteban

Sáb Nov 27, 2010 22:50
Matemática Financeira
-
- Pessoal não estou conseguindo resolver a questão da prova
por caahsmoreira » Qua Mar 12, 2014 01:01
- 1 Respostas
- 1757 Exibições
- Última mensagem por Russman

Qua Mar 12, 2014 12:23
Funções
-
- Amigos estou com dificuldades em resolver esse problema
por Catriane Moreira » Sáb Nov 20, 2010 22:54
- 1 Respostas
- 1600 Exibições
- Última mensagem por esteban

Sáb Nov 27, 2010 22:09
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
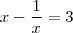
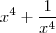
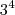 , mas acho que estou errado.
, mas acho que estou errado.
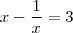
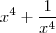
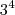 , mas acho que estou errado.
, mas acho que estou errado.
 . Agora, elevemos ao quadrado.
. Agora, elevemos ao quadrado.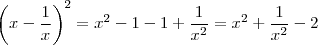
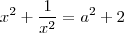 .
.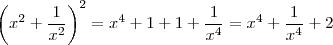
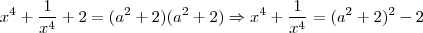 .
.
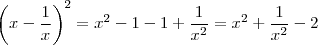
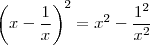

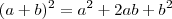 para todo a e b reais.
para todo a e b reais. 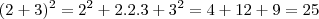
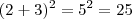 .
. e
e  .
.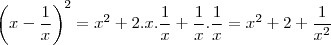



 .
.
 :
: