 por arnoanderson » Sáb Nov 28, 2009 12:14
por arnoanderson » Sáb Nov 28, 2009 12:14
Estou com dificuldade no seguinte problema
Um quadrado de lado L está se expandindo segundo a equação:
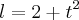
onde

Preciso encontrar a taxa de variação.(Que é a derivada, não?)
Sei que o resultado é 48, porém derivando a função e multiplicando pelos lados do quadrado não chego nesse valor. Somente chego ao valor 48 quando aplico diretamente a função, sem aplicar a derivada. Queria saber porquê.
Obrigado
(Obs, coloquei no tópico errado)
-
arnoanderson
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Nov 01, 2009 16:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Elcioschin » Sáb Nov 28, 2009 18:14
por Elcioschin » Sáb Nov 28, 2009 18:14
Acho que deve ser taxa de variação da área do quadrado, embora vc não tenha dito isto no enunciado:
L = 2 + t²
S = L² ----> S = (2 + t²)² ----> S = t^4 + 4*t² + 4
S' = 4*t³ + 8*t ----> S' = 4*(2³) + 4*(2²) ----> S' = 32 + 16 ----> S' = 48
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por arnoanderson » Seg Nov 30, 2009 19:29
por arnoanderson » Seg Nov 30, 2009 19:29
Oi Elcioschin.
É exatamente isso que você disse, taxa de variação da área do quadrado.
Tinha feito isso. O que me deixou na dúvida é que não derivei a função

, mas sim apliquei diretamente. Acredito que a dúvida nesse caso é mais "conceitual" mesmo. Quando é solicitada taxa de variação não é necessário derivar a função? Ex.Y=

-->
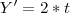
(Que daria outro resultado, errôneo nesse caso)
Isso que não entendi.
Obrigado!
-
arnoanderson
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Nov 01, 2009 16:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Elcioschin » Seg Nov 30, 2009 21:06
por Elcioschin » Seg Nov 30, 2009 21:06
arnoanderson
Primeiro vamos relembrar algo básico: A área S de um quadrado de lado L é dada por S = L².
O lado do quadrado do seu problema é uma função dada por L(t) = 2 + t²
Esta função mostra como varia o lado do quadrado com o tempo: note que o lado aumenta com o tempo.
Se você derivar a função acima você estará calculando a "taxa de variação do LADO do quadrado".
O que o problema pede é a "taxa de variação da ÁREA do quadrado"
Assim, você está derivando a função ERRADA.
À medida em que o lado do quadrado vai aumentando, a área dele também vai aumentando.
A área S(t) do quadrado será uma NOVA função, dada por:
S(t) = [L(t)]² -----> S(t) = (2 + t²)² ----> S(t) = t^4 + 4*t² + 4
Para saber qual é a "taxa de variação da ÁREA do quadrado" deve-se derivar esta NOVA função S(t):
S '(t) = 4*t³ + 8*t
Para t = 2 a "taxa de variação da ÁREA" valerá ----> S '(2) = 4*2³ + 8*2 -----> S '(2) = 48
Deu para entender agora?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADA] TAXA DE VARIAÇÃO - EXERCICIO DUVIDA
por OoluanOo » Dom Mar 03, 2013 18:02
- 1 Respostas
- 2359 Exibições
- Última mensagem por Russman

Dom Mar 03, 2013 19:58
Cálculo: Limites, Derivadas e Integrais
-
- [Taxa Sobre Taxa] Duvida...
por Myneyrynho » Qui Mar 21, 2013 11:56
- 1 Respostas
- 1530 Exibições
- Última mensagem por killua05

Qua Mai 29, 2013 13:16
Matemática Financeira
-
- Taxa de variação
por felipe_ad » Ter Jun 29, 2010 19:44
- 2 Respostas
- 60624 Exibições
- Última mensagem por Guill

Ter Fev 21, 2012 21:17
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de variação
 por AlbertoAM » Sáb Mai 21, 2011 14:23
por AlbertoAM » Sáb Mai 21, 2011 14:23
- 1 Respostas
- 5499 Exibições
- Última mensagem por LuizAquino

Dom Mai 22, 2011 13:03
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por AlbertoAM » Sáb Mai 28, 2011 15:53
por AlbertoAM » Sáb Mai 28, 2011 15:53
- 10 Respostas
- 10663 Exibições
- Última mensagem por AlbertoAM

Ter Mai 31, 2011 21:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
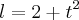




 , mas sim apliquei diretamente. Acredito que a dúvida nesse caso é mais "conceitual" mesmo. Quando é solicitada taxa de variação não é necessário derivar a função? Ex.Y=
, mas sim apliquei diretamente. Acredito que a dúvida nesse caso é mais "conceitual" mesmo. Quando é solicitada taxa de variação não é necessário derivar a função? Ex.Y= 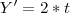 (Que daria outro resultado, errôneo nesse caso)
(Que daria outro resultado, errôneo nesse caso) em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.