 por Jhenrique » Qua Out 31, 2012 02:25
por Jhenrique » Qua Out 31, 2012 02:25
É muito comum realizarmos simplificações em cadeia como se segue abaixo...
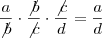
Mas o que eu gostaria de saber é se é possível relizar algum tipo de simplificação em cadeia do ponto de vista geométrico...
![\sqrt[\not{b}]{a}^{\sqrt[\not{c}]{\not{b}}^{\sqrt[d]{\not{c}}}} = \sqrt[d]{a} \sqrt[\not{b}]{a}^{\sqrt[\not{c}]{\not{b}}^{\sqrt[d]{\not{c}}}} = \sqrt[d]{a}](/latexrender/pictures/0a2b036645b0e167a8d3dbf77372bf3c.png)
Algo como isto acima, por exemplo....
Obg!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Qua Out 31, 2012 07:13
por MarceloFantini » Qua Out 31, 2012 07:13
Escreva os expoentes como frações e veja se há cancelamentos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Qua Out 31, 2012 18:18
por Jhenrique » Qua Out 31, 2012 18:18
Eu sei, não há!
Esse exemplo foi apenas um modelo para a minha pergunta.
Essa questão me surgiu quando eu destingui o coneito de Taxa de Variação Geométrica do conceito de Taxa de Variação Aritmética.
Se não é possível formular uma regra da cadeia geométrica então não existe regra da cadeia para o
![\lim_{\Delta x->0} \sqrt[\Delta x]{\Delta y} \lim_{\Delta x->0} \sqrt[\Delta x]{\Delta y}](/latexrender/pictures/774e186fb5292c9112d97da1d160e692.png)
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- lei do cancelamento universal do estudante
por admin » Qua Set 10, 2008 18:19
- 1 Respostas
- 5329 Exibições
- Última mensagem por Neperiano

Sex Set 16, 2011 19:51
Piadas
-
- Leis do Cancelamento em Domínios de Integridade
por m0x0 » Sáb Jul 23, 2011 20:18
- 0 Respostas
- 1844 Exibições
- Última mensagem por m0x0

Sáb Jul 23, 2011 20:18
Álgebra Elementar
-
- [ regra da cadeia ]
por Marimar » Seg Nov 07, 2011 13:34
- 3 Respostas
- 3061 Exibições
- Última mensagem por MarceloFantini

Seg Nov 07, 2011 14:37
Cálculo: Limites, Derivadas e Integrais
-
- Regra da Cadeia
por Cleyson007 » Ter Mai 22, 2012 15:17
- 1 Respostas
- 1889 Exibições
- Última mensagem por joaofonseca

Ter Mai 22, 2012 19:14
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas- regra da cadeia
por genicleide » Qua Abr 20, 2011 14:28
- 4 Respostas
- 4948 Exibições
- Última mensagem por genicleide

Qua Abr 20, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
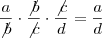
![\sqrt[\not{b}]{a}^{\sqrt[\not{c}]{\not{b}}^{\sqrt[d]{\not{c}}}} = \sqrt[d]{a} \sqrt[\not{b}]{a}^{\sqrt[\not{c}]{\not{b}}^{\sqrt[d]{\not{c}}}} = \sqrt[d]{a}](/latexrender/pictures/0a2b036645b0e167a8d3dbf77372bf3c.png)

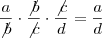
![\sqrt[\not{b}]{a}^{\sqrt[\not{c}]{\not{b}}^{\sqrt[d]{\not{c}}}} = \sqrt[d]{a} \sqrt[\not{b}]{a}^{\sqrt[\not{c}]{\not{b}}^{\sqrt[d]{\not{c}}}} = \sqrt[d]{a}](/latexrender/pictures/0a2b036645b0e167a8d3dbf77372bf3c.png)



![\lim_{\Delta x->0} \sqrt[\Delta x]{\Delta y} \lim_{\Delta x->0} \sqrt[\Delta x]{\Delta y}](/latexrender/pictures/774e186fb5292c9112d97da1d160e692.png)

