 por daianalemos10 » Ter Jan 21, 2014 14:45
por daianalemos10 » Ter Jan 21, 2014 14:45
Reais e complexos são isomorfos como aneis?
mostre que Q
![sqrt[2] e Q sqrt[3] sqrt[2] e Q sqrt[3]](/latexrender/pictures/9e6606822b66f83f46010ec762e0385b.png)
não são isomorfos.
Sejam R e S aneis comutativos com unidade. Se
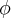
é um homomorfismo de R sobre S e a caracteristica de R é não nula, prove que a caracteristica de S divide a caracteristica de R.
(não sei nem como começar)
-
daianalemos10
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jan 21, 2014 11:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura matematica
- Andamento: cursando
 por adauto martins » Qua Dez 28, 2016 17:08
por adauto martins » Qua Dez 28, 2016 17:08
seja
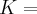
{
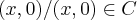
},onde C é o conj.numeros complexos,a saber:
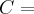
{
![z=(x,y)/z=x+yi,i=\sqrt[]{-1} z=(x,y)/z=x+yi,i=\sqrt[]{-1}](/latexrender/pictures/621b7a84e98f5f7e57adb73c7a3e3dc7.png)
}...vamos tomar
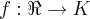
e tal q.
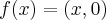
,entao:
1)
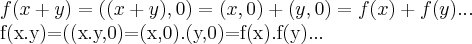
,logo f e homomorfica...
pela definiçao de f,temos que:
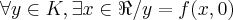
,ou seja ,f é sobrejetiva,logo f é um isomorfismo...em geral,temos que:


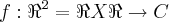
é um isomorfismo(prove isso!)...
agora:
![f:Q[\sqrt[]{2}]\rightarrow Q[\sqrt[]{3}] f:Q[\sqrt[]{2}]\rightarrow Q[\sqrt[]{3}]](/latexrender/pictures/2035eda00fcda6bc7e1c9095d9694ae2.png)
,nao é um isomorfismo,pois:
sabemos que:
![Q[\sqrt[]{2}]= Q[\sqrt[]{2}]=](/latexrender/pictures/a7256f5f86c336331eb74188f74ad173.png)
{
![p+q\sqrt[]{2} p+q\sqrt[]{2}](/latexrender/pictures/61adc756d326f219893de9b078683fbc.png)
![p+q\sqrt[]{2}/p,q \in Q p+q\sqrt[]{2}/p,q \in Q](/latexrender/pictures/cc52592197311a5267ec9d00bbe70af5.png)
}...
![Q[\sqrt[]{3}]= Q[\sqrt[]{3}]=](/latexrender/pictures/e869a99ce70e7960638a95734722586d.png)
{
![m+n\sqrt[]{3}/m,n \in Q m+n\sqrt[]{3}/m,n \in Q](/latexrender/pictures/f0da65fec32e79ce293c569b21656290.png)
}...
suponhamos q.:
![f:Q[\sqrt[]{2}]\rightarrow Q[\sqrt[]{3}] f:Q[\sqrt[]{2}]\rightarrow Q[\sqrt[]{3}]](/latexrender/pictures/2035eda00fcda6bc7e1c9095d9694ae2.png)
seja um isomorfismo,logo:
![f(2)=f(\sqrt[]{2}.\sqrt[]{2})=a+b\sqrt[]{3} f(2)=f(\sqrt[]{2}.\sqrt[]{2})=a+b\sqrt[]{3}](/latexrender/pictures/631669dab169909fdb971959704d4b08.png)
,como f é um isomorfismo,teriamos entao q.:
![f(1)=1...f(2)=f(1+1)=f(1)+f(1)=2...se:
[tex]{f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais) f(1)=1...f(2)=f(1+1)=f(1)+f(1)=2...se:
[tex]{f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais)](/latexrender/pictures/cee47d65bc316d4028a33a0f72c3400f.png)
![{f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais) {f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais)](/latexrender/pictures/f5721acbc42bcd3a03838d7e3c668b6a.png)
,logo uma contradiçao...entao f nao é um homomorfismo,e como consequencia nao é um isomorfismo...


é por hipotese um homomorfismo,logo é injetivo,entao:
![NUC[\phi]= NUC[\phi]=](/latexrender/pictures/e714dcd144369ad5f1d4e28d9e6d9038.png)
{
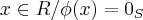
}...entao:
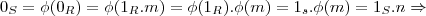
existe
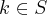
,tal que k divide
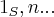
,como
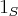
divide apenas ele proprio,logo n=km...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Assuntos Gerais] Bacharelando ou Licenciatura.
por Pessoa Estranha » Ter Ago 13, 2013 20:23
- 6 Respostas
- 7156 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 22, 2013 14:50
Assuntos Gerais ou OFF-TOPIC
-
- Algebra Linear para resolução de Conjutos
por SuPr3MeMoTF » Qui Out 15, 2015 17:11
- 1 Respostas
- 2077 Exibições
- Última mensagem por adauto martins

Qui Out 15, 2015 19:11
Álgebra Linear
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3705 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
-
- onde a funcao tem concavidade para cima e para baixo?
por tumiattibrz » Sáb Jun 04, 2011 01:00
- 4 Respostas
- 4677 Exibições
- Última mensagem por Fabio Cabral

Seg Jun 06, 2011 23:54
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Funciona para produto mas não para quociente?
por Matheus Lacombe O » Ter Dez 11, 2012 23:46
- 1 Respostas
- 2190 Exibições
- Última mensagem por Russman

Qua Dez 12, 2012 01:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![sqrt[2] e Q sqrt[3] sqrt[2] e Q sqrt[3]](/latexrender/pictures/9e6606822b66f83f46010ec762e0385b.png) não são isomorfos.
não são isomorfos.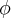 é um homomorfismo de R sobre S e a caracteristica de R é não nula, prove que a caracteristica de S divide a caracteristica de R.
é um homomorfismo de R sobre S e a caracteristica de R é não nula, prove que a caracteristica de S divide a caracteristica de R.
![sqrt[2] e Q sqrt[3] sqrt[2] e Q sqrt[3]](/latexrender/pictures/9e6606822b66f83f46010ec762e0385b.png) não são isomorfos.
não são isomorfos.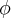 é um homomorfismo de R sobre S e a caracteristica de R é não nula, prove que a caracteristica de S divide a caracteristica de R.
é um homomorfismo de R sobre S e a caracteristica de R é não nula, prove que a caracteristica de S divide a caracteristica de R.
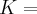 {
{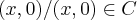 },onde C é o conj.numeros complexos,a saber:
},onde C é o conj.numeros complexos,a saber: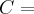 {
{![z=(x,y)/z=x+yi,i=\sqrt[]{-1} z=(x,y)/z=x+yi,i=\sqrt[]{-1}](/latexrender/pictures/621b7a84e98f5f7e57adb73c7a3e3dc7.png) }...vamos tomar
}...vamos tomar 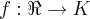 e tal q.
e tal q.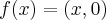 ,entao:
,entao: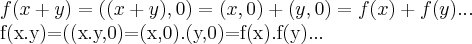 ,logo f e homomorfica...
,logo f e homomorfica...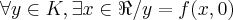 ,ou seja ,f é sobrejetiva,logo f é um isomorfismo...em geral,temos que:
,ou seja ,f é sobrejetiva,logo f é um isomorfismo...em geral,temos que:

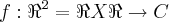 é um isomorfismo(prove isso!)...
é um isomorfismo(prove isso!)...![f:Q[\sqrt[]{2}]\rightarrow Q[\sqrt[]{3}] f:Q[\sqrt[]{2}]\rightarrow Q[\sqrt[]{3}]](/latexrender/pictures/2035eda00fcda6bc7e1c9095d9694ae2.png) ,nao é um isomorfismo,pois:
,nao é um isomorfismo,pois:![Q[\sqrt[]{2}]= Q[\sqrt[]{2}]=](/latexrender/pictures/a7256f5f86c336331eb74188f74ad173.png) {
{![p+q\sqrt[]{2} p+q\sqrt[]{2}](/latexrender/pictures/61adc756d326f219893de9b078683fbc.png)
![p+q\sqrt[]{2}/p,q \in Q p+q\sqrt[]{2}/p,q \in Q](/latexrender/pictures/cc52592197311a5267ec9d00bbe70af5.png) }...
}...![Q[\sqrt[]{3}]= Q[\sqrt[]{3}]=](/latexrender/pictures/e869a99ce70e7960638a95734722586d.png) {
{![m+n\sqrt[]{3}/m,n \in Q m+n\sqrt[]{3}/m,n \in Q](/latexrender/pictures/f0da65fec32e79ce293c569b21656290.png) }...
}...![f:Q[\sqrt[]{2}]\rightarrow Q[\sqrt[]{3}] f:Q[\sqrt[]{2}]\rightarrow Q[\sqrt[]{3}]](/latexrender/pictures/2035eda00fcda6bc7e1c9095d9694ae2.png) seja um isomorfismo,logo:
seja um isomorfismo,logo:![f(2)=f(\sqrt[]{2}.\sqrt[]{2})=a+b\sqrt[]{3} f(2)=f(\sqrt[]{2}.\sqrt[]{2})=a+b\sqrt[]{3}](/latexrender/pictures/631669dab169909fdb971959704d4b08.png) ,como f é um isomorfismo,teriamos entao q.:
,como f é um isomorfismo,teriamos entao q.:![f(1)=1...f(2)=f(1+1)=f(1)+f(1)=2...se:
[tex]{f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais) f(1)=1...f(2)=f(1+1)=f(1)+f(1)=2...se:
[tex]{f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais)](/latexrender/pictures/cee47d65bc316d4028a33a0f72c3400f.png)
![{f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais) {f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais)](/latexrender/pictures/f5721acbc42bcd3a03838d7e3c668b6a.png) ,logo uma contradiçao...entao f nao é um homomorfismo,e como consequencia nao é um isomorfismo...
,logo uma contradiçao...entao f nao é um homomorfismo,e como consequencia nao é um isomorfismo...
 é por hipotese um homomorfismo,logo é injetivo,entao:
é por hipotese um homomorfismo,logo é injetivo,entao:![NUC[\phi]= NUC[\phi]=](/latexrender/pictures/e714dcd144369ad5f1d4e28d9e6d9038.png) {
{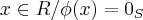 }...entao:
}...entao: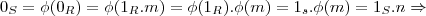 existe
existe 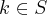 ,tal que k divide
,tal que k divide 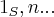 ,como
,como 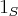 divide apenas ele proprio,logo n=km...
divide apenas ele proprio,logo n=km...





