Determine todos os pares
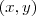 de inteiros positivos que satisfazem a equação
de inteiros positivos que satisfazem a equação .
.OBS.:Considerei essa equação como uma equação do segundo grau em
 ( já que
( já que 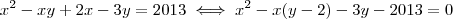 ), donde
), donde  .Aí depois eu não sei mais como prosseguir a resolução!!!Desde já, muito obrigado pela ajuda!!!
.Aí depois eu não sei mais como prosseguir a resolução!!!Desde já, muito obrigado pela ajuda!!!

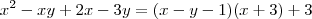
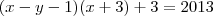
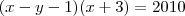
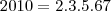 , então
, então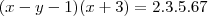
 e
e 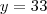 . Eu fiz
. Eu fiz 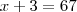 e
e 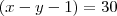 de onde segue. Agora basta calcular os outros. Eu ACHO que a quantidade de pares será a combinação de 4, 2 a 2 multiplicada pela combinação de 4, 3 a 3. Ou seja, 24 pares diferentes. Mas não tenho certeza.
de onde segue. Agora basta calcular os outros. Eu ACHO que a quantidade de pares será a combinação de 4, 2 a 2 multiplicada pela combinação de 4, 3 a 3. Ou seja, 24 pares diferentes. Mas não tenho certeza.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)