 por b_afa » Sex Nov 22, 2013 17:52
por b_afa » Sex Nov 22, 2013 17:52
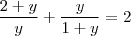
O cara fez
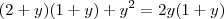
-->
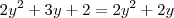
-->
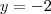
Não entendi porque multiplicar cruzado se é uma soma... e porque multiplicar 2 por y e (1+y)?
Editado pela última vez por
b_afa em Sex Nov 22, 2013 18:44, em um total de 1 vez.
-
b_afa
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Nov 15, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando \o/
- Andamento: cursando
 por Cleyson007 » Sex Nov 22, 2013 18:07
por Cleyson007 » Sex Nov 22, 2013 18:07
Boa tarde b_afa!
Na verdade, o cara tirou o m.m.c. A regra é a seguinte: Pega o seu m.m.c, divide no denominador e multiplica no numerador. Feito isso, você pode descartá-lo, acompanhe:
m.m.c entre
y e
y+1 é: y (y + 1)
(y + 1) (
2y) + y² = 2y (y+1) --> A parte em vermelho você digitou errado.
Agora é só resolver

Te enviei uma mensagem privada, por favor me responda. Ok?
Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por b_afa » Sex Nov 22, 2013 18:45
por b_afa » Sex Nov 22, 2013 18:45
Cleyson007 escreveu:Boa tarde b_afa!
Na verdade, o cara tirou o m.m.c. A regra é a seguinte: Pega o seu m.m.c, divide no denominador e multiplica no numerador. Feito isso, você pode descartá-lo, acompanhe:
m.m.c entre
y e
y+1 é: y (y + 1)
(y + 1) (
2y) + y² = 2y (y+1) --> A parte em vermelho você digitou errado.
Agora é só resolver

Te enviei uma mensagem privada, por favor me responda. Ok?
Abraço,
Cleyson007
Realmente,eu digitei a primeira fração errado,é 2+y e não 2y.Obrigado pela ajuda! Vi sua mensagem mas diz que eu não tem "autorização para enviar uma mensagem"...
-
b_afa
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Nov 15, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando \o/
- Andamento: cursando
 por Cleyson007 » Sex Nov 22, 2013 23:12
por Cleyson007 » Sex Nov 22, 2013 23:12
b_afa, me envie por e-mail então:
descomplicamat@hotmail.com
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Soma de frações algébricas, como igualar os denominadores?
por lucas7 » Qui Fev 17, 2011 20:55
- 5 Respostas
- 4215 Exibições
- Última mensagem por Cleyson007

Sex Fev 18, 2011 18:23
Álgebra Elementar
-
- Integral da soma/Soma das Integrais.
por Sobreira » Ter Abr 30, 2013 17:41
- 0 Respostas
- 2101 Exibições
- Última mensagem por Sobreira

Ter Abr 30, 2013 17:41
Cálculo: Limites, Derivadas e Integrais
-
- [Frações] Regra de frações
por raymondtfr » Dom Nov 02, 2014 16:49
- 4 Respostas
- 3326 Exibições
- Última mensagem por Russman

Dom Nov 02, 2014 23:57
Aritmética
-
- FRAÇÕES
por csantos » Sex Ago 29, 2008 16:33
- 1 Respostas
- 3265 Exibições
- Última mensagem por admin

Sex Ago 29, 2008 16:47
Álgebra Elementar
-
- frações
por suryah » Qua Out 20, 2010 18:28
- 3 Respostas
- 3580 Exibições
- Última mensagem por DanielFerreira

Seg Nov 29, 2010 19:54
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
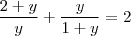
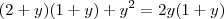 -->
--> 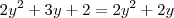 -->
-->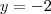

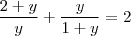
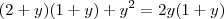 -->
--> 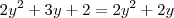 -->
-->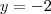






 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
