 por TLWeber » Sáb Out 26, 2013 20:53
por TLWeber » Sáb Out 26, 2013 20:53
Boa noite preciso ajuda em duas questões sobre matrizes
1ª Questão sendo:
A=
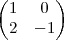
B=
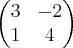
C=
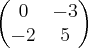
determine:
a) A.B.C
OBS sei que para fazer a multiplicação é linha vezes coluna mas nao fechou podem me ajudar?!
2ª Questão Dadas as matrizes A= (aij) 6x4, tal que aij= i-j, B= (bij)4x5, tal que bij= j-i e C=AB, determine o elemento C42
a resposta é 2
alguem poderia me mostrar como faze-la? pois nao entendi a mesma
-
TLWeber
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Set 22, 2013 23:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sáb Out 26, 2013 22:29
por e8group » Sáb Out 26, 2013 22:29
Na questão 2 . Observe que pela definição de produto entre matrizes que o termo geral da matriz C=AB é dado por :
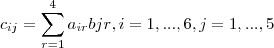
.Utilizando que ,
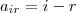
e
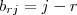
,segue
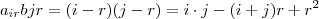
.
Logo ,
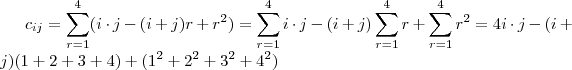
.
Daí ,
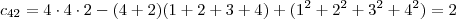
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5168 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3606 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 6005 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- matrizes
por luix henrique » Seg Out 13, 2008 15:42
- 1 Respostas
- 9699 Exibições
- Última mensagem por Molina

Seg Out 13, 2008 20:13
Matrizes e Determinantes
-
- Matrizes
por Giles » Qua Out 29, 2008 23:24
- 7 Respostas
- 12818 Exibições
- Última mensagem por Molina

Sex Nov 14, 2008 01:24
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
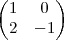
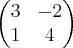
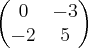 determine:
determine: 

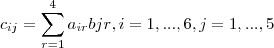 .Utilizando que ,
.Utilizando que , 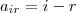 e
e 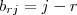 ,segue
,segue 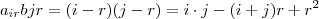 .
. 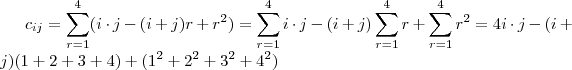 .
. 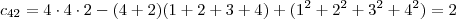 .
.