Seja R a relação:
![R=[(a,b)\in Z x Z | ab>0] \cup [(0,0)] R=[(a,b)\in Z x Z | ab>0] \cup [(0,0)]](/latexrender/pictures/7810a97230f47dc93a7cd0576b590e0b.png) (obs: o x representa multiplicação, e os colchetes na verdade são chaves, mas não quis sair na formatação.)
(obs: o x representa multiplicação, e os colchetes na verdade são chaves, mas não quis sair na formatação.)Mostrar que R é uma rel. de equivalência em Z;
Exibir a partição de Z pela relação de equivalência R.
Valeu

![R=[(a,b)\in Z x Z | ab>0] \cup [(0,0)] R=[(a,b)\in Z x Z | ab>0] \cup [(0,0)]](/latexrender/pictures/7810a97230f47dc93a7cd0576b590e0b.png) (obs: o x representa multiplicação, e os colchetes na verdade são chaves, mas não quis sair na formatação.)
(obs: o x representa multiplicação, e os colchetes na verdade são chaves, mas não quis sair na formatação.)
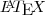 tens que digitar uma barra antes. Por exemplo, \{ e \}.
tens que digitar uma barra antes. Por exemplo, \{ e \}.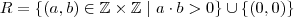
 .
.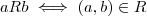 .
.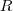 particiona
particiona  em três classes de equivalência:
em três classes de equivalência:![[1]=\{a\in\mathbb{Z}\mid aR1\}=\mathbb{Z}^*_+=\{a\in\mathbb{Z}\mid a>0\} [1]=\{a\in\mathbb{Z}\mid aR1\}=\mathbb{Z}^*_+=\{a\in\mathbb{Z}\mid a>0\}](/latexrender/pictures/5fba8a6f172f6c0eb0447d392197b125.png)
![[0]=\{a\in\mathbb{Z}\mid aR0\}=\{0\} [0]=\{a\in\mathbb{Z}\mid aR0\}=\{0\}](/latexrender/pictures/4bc86b9b14afeb11c15f14d1b0faff62.png)
![[-1]=\{a\in\mathbb{Z}\mid aR(-1)\}=\mathbb{Z}^*_-=\{a\in\mathbb{Z}\mid a<0\} [-1]=\{a\in\mathbb{Z}\mid aR(-1)\}=\mathbb{Z}^*_-=\{a\in\mathbb{Z}\mid a<0\}](/latexrender/pictures/f35db6dac2f5c89e9f18aac642076ae0.png)
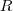 , pois, para quaisquer números positivos
, pois, para quaisquer números positivos  e
e  teremos
teremos 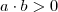 , ou seja,
, ou seja, 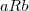 .
.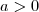 e
e 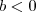 , então
, então 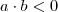 .
.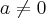 tal que
tal que 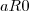 , então
, então 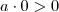 , absurdo. Por outro lado, como
, absurdo. Por outro lado, como 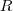 é uma relação de equivalência (que é o que você terá que provar), pela propriedade reflexiva teremos
é uma relação de equivalência (que é o que você terá que provar), pela propriedade reflexiva teremos 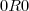 , o que se vê imediatamente pela definição de
, o que se vê imediatamente pela definição de 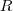 , pois
, pois 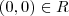 .
.

![[0] [0]](/latexrender/pictures/8d5162ca104fa7e79fe80fd92bb657fb.png) . Nas partições
. Nas partições ![[1] [1]](/latexrender/pictures/35dba5d75538a9bbe0b4da4422759a0e.png) e
e ![[-1] [-1]](/latexrender/pictures/edb06daebcc6f079a6dee9a7ed831ea9.png) existem infinitos números porque
existem infinitos números porque ![[1] [1]](/latexrender/pictures/35dba5d75538a9bbe0b4da4422759a0e.png) contém todos números inteiros positivos e
contém todos números inteiros positivos e ![[-1] [-1]](/latexrender/pictures/edb06daebcc6f079a6dee9a7ed831ea9.png) contém todos números inteiros negativos. Acho que a minha notação acabou te confundindo. Quando representei uma classe que equivalencia por
contém todos números inteiros negativos. Acho que a minha notação acabou te confundindo. Quando representei uma classe que equivalencia por ![[1] [1]](/latexrender/pictures/35dba5d75538a9bbe0b4da4422759a0e.png) , por exemplo, quis represe ntar que todos os elementos dessa classe são equivalentes ao
, por exemplo, quis represe ntar que todos os elementos dessa classe são equivalentes ao  , mas não que o
, mas não que o  é o único elemento. Poderíamos muito bem representar a classe de equivalência
é o único elemento. Poderíamos muito bem representar a classe de equivalência ![[1] [1]](/latexrender/pictures/35dba5d75538a9bbe0b4da4422759a0e.png) , por exemplo, como
, por exemplo, como ![[2] [2]](/latexrender/pictures/beb4dbf9af069aa2df7b147229965085.png) ,
, ![[3] [3]](/latexrender/pictures/f2577a6fc29b900fe7d4c6321346be48.png) ,
, ![[1000] [1000]](/latexrender/pictures/823c8332a9da982601bde78f82bffdee.png) , ou por qualquer representação
, ou por qualquer representação ![[x] [x]](/latexrender/pictures/3e5314e9fd31509fdeb83faa0f729ba2.png) , com
, com  sendo um inteiro positivo, porque vimos que todos os inteiros positivos são equivalentes pela relação de equivalência
sendo um inteiro positivo, porque vimos que todos os inteiros positivos são equivalentes pela relação de equivalência 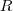 .
.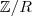 é o conjunto de todas as classes de equivalência em
é o conjunto de todas as classes de equivalência em  pela relação de equivalência
pela relação de equivalência 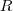 .
.![\mathbb{Z}/R=\{[-1],\ [0],\ [1]\}=\{\mathbb{Z}_-^*,\ \{0\},\ \mathbb{Z}_+^*\} \mathbb{Z}/R=\{[-1],\ [0],\ [1]\}=\{\mathbb{Z}_-^*,\ \{0\},\ \mathbb{Z}_+^*\}](/latexrender/pictures/1abed4c1b7ae93efbd22737f0d241294.png)

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)