 por Mimizinha » Qui Mar 20, 2008 10:09
por Mimizinha » Qui Mar 20, 2008 10:09
10. Uma feirante vende seu produto com margem de lucro de 40% sobre o preço de custo. Se adquirir a unidade por R$2,00, qual a quantidade que deverá vender para lucrar no mínimo R$ 120,00?
L= Px40%x2,00
120= Px0,4x2,00
120= 0,8P
P= 150
Desde já agradeço
-
Mimizinha
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Qua Mar 19, 2008 13:50
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Qui Mar 20, 2008 12:02
por admin » Qui Mar 20, 2008 12:02
Olá.
Está correto sim.
Nestes problemas sempre tenha cuidado começando pelo elementar, assim você minimiza a chance de errar:
lucro = total de venda - total de custo
Se
l: lucro
v: total de venda
c: total de custo
p: quantidade de produtos
Então:
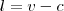
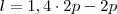
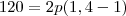
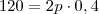
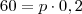
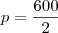

produtos
Citei estes passos também para exemplificar como facilitar e agilizar as contas mentalmente.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Mimizinha » Qui Mar 20, 2008 12:16
por Mimizinha » Qui Mar 20, 2008 12:16
De onde veio esse 1,4?
-
Mimizinha
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Qua Mar 19, 2008 13:50
- Área/Curso: Estudante
- Andamento: cursando
 por Mimizinha » Qui Mar 20, 2008 13:00
por Mimizinha » Qui Mar 20, 2008 13:00
Agora sim entendi.
Obrigada
-
Mimizinha
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Qua Mar 19, 2008 13:50
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Gostaria de saber, como surgiu esta formula.
por bencz » Qui Jul 14, 2011 00:27
- 1 Respostas
- 1862 Exibições
- Última mensagem por Molina

Dom Jul 17, 2011 15:10
Geometria Analítica
-
- Gostaria de saber como calcular o seguinte limite
por felipe_08 » Qui Abr 23, 2015 17:36
- 2 Respostas
- 2582 Exibições
- Última mensagem por felipe_08

Qui Abr 23, 2015 22:51
Cálculo: Limites, Derivadas e Integrais
-
- gostaria de saber como fazer exercicio sobre estatiscas?
por edilmawesley » Ter Set 06, 2011 02:23
- 0 Respostas
- 1259 Exibições
- Última mensagem por edilmawesley

Ter Set 06, 2011 02:23
Estatística
-
- [Limite] Gostaria de saber se posso operar dessa maneira.
por ravi » Ter Out 09, 2012 10:50
- 5 Respostas
- 3866 Exibições
- Última mensagem por LuizAquino

Qui Out 11, 2012 23:37
Cálculo: Limites, Derivadas e Integrais
-
- Quero saber se minha resposta está correta
por Raquel299 » Seg Mar 09, 2015 09:53
- 3 Respostas
- 2747 Exibições
- Última mensagem por Raquel299

Sex Abr 10, 2015 10:49
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


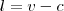
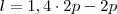
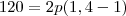
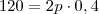
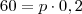
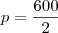
 produtos
produtos

 em evidência:
em evidência: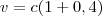
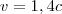
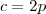
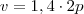


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.