Por exemplo , segue uma questão a seguir que o objetivo é identificar o erro na solução feito por um aluno .
Dada a inequação modular
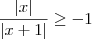
Solução.
i)

ii)
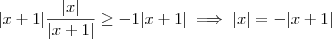
iii)
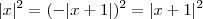
iv) Como
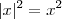 e
e  Segue que
Segue que 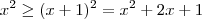 que da como solução
que da como solução 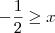
Não tenho o gabarito , mas analisando acredito que o erro está na etapa ( iii) . Não estou conseguindo formula um argumento que prove o erro dele . Por favor , alguém descorda ? Se não , qual argumento você usaria ?
Entretanto quando eu começo desenvolver a questão desde o ponto inicial , eu consigo mostrar que todos valores reais exceto
 satisfaz
satisfaz 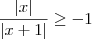 . Como segue a segue os passos a seguir .
. Como segue a segue os passos a seguir . De fato ,
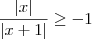 . Pois ,
. Pois , 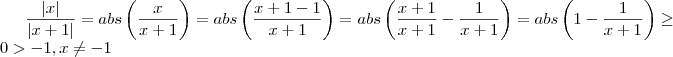 .
. Quando
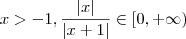 e quando
e quando 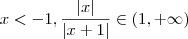 , ou seja para quaisquer
, ou seja para quaisquer 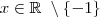 temos que
temos que 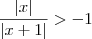
OBS. Usei abs para modulo , por causa da configuração da barra .


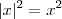 e
e  . Isso é verdade , mas
. Isso é verdade , mas 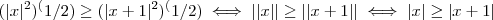 .O que não é verdade para x diferente que - 1 .
.O que não é verdade para x diferente que - 1 .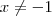 . Segundo, já está errado na segunda etapa. Teremos
. Segundo, já está errado na segunda etapa. Teremos 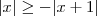 , não igual. Tome
, não igual. Tome  . Então é claro que
. Então é claro que 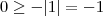 , mas
, mas 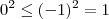 , não maior ou igual. Então o processo de elevar ao quadrado está errado.
, não maior ou igual. Então o processo de elevar ao quadrado está errado. ,
, 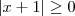 e portanto
e portanto 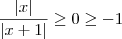 para todo
para todo  ,
, 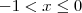 e
e  .
.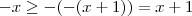 , daí
, daí 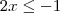 e
e 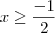 . Como assumimos
. Como assumimos 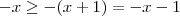 , que nos leva a
, que nos leva a 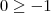 que é verdadeiro sempre. Portanto
que é verdadeiro sempre. Portanto 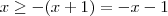 , que nos leva a
, que nos leva a  e
e  , todo valor é solução.
, todo valor é solução.

