 por DanielFerreira » Sáb Mai 05, 2012 23:57
por DanielFerreira » Sáb Mai 05, 2012 23:57
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizCarlos » Dom Mai 06, 2012 00:23
por LuizCarlos » Dom Mai 06, 2012 00:23
Olá amigo danjr5, obrigado por sempre me ajudar, você é uma ótima pessoa! na terceira igualdade existe um produto notável no numerador:
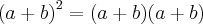
, somente fiz isso!
Mas a resposta no livro não é a mesma que a nossa!
A reposta no livro é:
![\sqrt[]{\frac{{a}^{2}+ ab}{{a}^{2}+ {b}^{2}}} \sqrt[]{\frac{{a}^{2}+ ab}{{a}^{2}+ {b}^{2}}}](/latexrender/pictures/a143dae7d1cd1b8e6c9407999013e30b.png)
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por DanielFerreira » Dom Mai 06, 2012 15:27
por DanielFerreira » Dom Mai 06, 2012 15:27
Então, o gabarito do seu livro está errado!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizCarlos » Dom Mai 06, 2012 19:30
por LuizCarlos » Dom Mai 06, 2012 19:30
danjr5 escreveu:Então, o gabarito do seu livro está errado!!
Creio que esteja mesmo, já fiz e refiz essa questão várias vezes, e somente encontro o mesmo resultado! obrigado amigo.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por DanielFerreira » Seg Mai 07, 2012 02:09
por DanielFerreira » Seg Mai 07, 2012 02:09
Não há de quê.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em exercício - raízes de função quadrática
por Danilo » Qui Jun 07, 2012 01:50
- 1 Respostas
- 3190 Exibições
- Última mensagem por Russman

Qui Jun 07, 2012 03:32
Funções
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8123 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- [Radiciação] Raízes dentro de raízes
por mottasky » Ter Set 13, 2011 22:00
- 2 Respostas
- 2583 Exibições
- Última mensagem por mottasky

Qui Set 15, 2011 15:52
Álgebra Elementar
-
- raízes.
por carolina camargo » Qua Jun 17, 2009 16:39
- 5 Respostas
- 2969 Exibições
- Última mensagem por Molina

Qua Jun 17, 2009 19:01
Funções
-
- Raízes
por aline2010 » Dom Ago 08, 2010 07:46
- 1 Respostas
- 1333 Exibições
- Última mensagem por MarceloFantini

Seg Ago 09, 2010 06:08
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![(a+b).\sqrt[]{\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{{(a+b)}^{2}}.\sqrt[]{\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{(a+b).\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{\frac{(a+b).(a+b).a}{(a+b).(a-b)}} (a+b).\sqrt[]{\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{{(a+b)}^{2}}.\sqrt[]{\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{(a+b).\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{\frac{(a+b).(a+b).a}{(a+b).(a-b)}}](/latexrender/pictures/037028f8252496934b475df5f6dba29f.png)
![= \sqrt[]{\frac{{a}^{2}+ab}{a-b}} = \sqrt[]{\frac{{a}^{2}+ab}{a-b}}](/latexrender/pictures/0b191216c1bf61bf885c2e1ee612a1d0.png)

![(a+b).\sqrt[]{\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{{(a+b)}^{2}}.\sqrt[]{\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{(a+b).\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{\frac{(a+b).(a+b).a}{(a+b).(a-b)}} (a+b).\sqrt[]{\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{{(a+b)}^{2}}.\sqrt[]{\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{(a+b).\frac{a}{{a}^{2}-{b}^{2}}} = \sqrt[]{\frac{(a+b).(a+b).a}{(a+b).(a-b)}}](/latexrender/pictures/037028f8252496934b475df5f6dba29f.png)
![= \sqrt[]{\frac{{a}^{2}+ab}{a-b}} = \sqrt[]{\frac{{a}^{2}+ab}{a-b}}](/latexrender/pictures/0b191216c1bf61bf885c2e1ee612a1d0.png)

![(a + b)\sqrt[]{\left[\frac{a}{a^2 - b^2} \right]} = (a + b)\sqrt[]{\left[\frac{a}{a^2 - b^2} \right]} =](/latexrender/pictures/8593f08f478b6dd27b7420fcf3b9caae.png)
![\sqrt[]{(a + b)^2.\left[\frac{a}{a^2 - b^2} \right]} = \sqrt[]{(a + b)^2.\left[\frac{a}{a^2 - b^2} \right]} =](/latexrender/pictures/a9e4274cb6739664ce06678552614dc7.png)
![\sqrt[]{\left[\frac{a(a + b)^2}{(a + b)(a - b)} \right]} = \sqrt[]{\left[\frac{a(a + b)^2}{(a + b)(a - b)} \right]} =](/latexrender/pictures/fc8c2515ee10af4afa910d42816fa3a6.png)
![\sqrt[]{\frac{a(a + b)}{(a - b)}} = \sqrt[]{\frac{a(a + b)}{(a - b)}} =](/latexrender/pictures/1f38fe4ad250aed437f36eac05cea781.png)

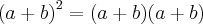 , somente fiz isso!
, somente fiz isso!![\sqrt[]{\frac{{a}^{2}+ ab}{{a}^{2}+ {b}^{2}}} \sqrt[]{\frac{{a}^{2}+ ab}{{a}^{2}+ {b}^{2}}}](/latexrender/pictures/a143dae7d1cd1b8e6c9407999013e30b.png)





 .
.



