


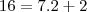 agora divida todos por 7 e obteremos
agora divida todos por 7 e obteremos 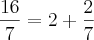 . supondo que vc ja saiba a estrutura da representaçao de um fraçao continuada, tremos: 2 + 2/7 transformando a fraçao temos: 2 +
. supondo que vc ja saiba a estrutura da representaçao de um fraçao continuada, tremos: 2 + 2/7 transformando a fraçao temos: 2 + 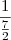 , efetuando a divisao e invertendo vamos encontrar como ultimo numerador da ultima fraçao o nemro 1. teremos:
, efetuando a divisao e invertendo vamos encontrar como ultimo numerador da ultima fraçao o nemro 1. teremos: 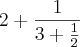 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.