 por Marlene » Ter Out 18, 2011 00:08
por Marlene » Ter Out 18, 2011 00:08
Quais números inteiros positivos menores que 120 podem ser escritos como soma de
duas ou mais potências distintas de base 3 e exponente inteiro maiores do que zero?
DETALHE NÃO SEI POSTAR MINHAS DUVIDAS?
-
Marlene
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Out 17, 2011 23:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura matematica
- Andamento: formado
 por LuizAquino » Ter Out 18, 2011 09:45
por LuizAquino » Ter Out 18, 2011 09:45
Marlene escreveu:Quais números inteiros positivos menores que 120 podem ser escritos como soma de
duas ou mais potências distintas de base 3 e exponente inteiro maiores do que zero?
Note que as parcelas devem ser menores do que
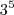
.
Portanto, você pode usar as potências
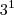
,
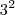
,
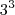
e
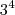
.
Usando duas dessas potências, você pode formar seis números distintos.
Já usando três dessas potências, você pode formar quatro números distintos.
Por fim, você não poderá usar as quatro potências juntas, pois
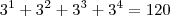
.
Agora basta você listar os números.
Marlene escreveu:DETALHE NÃO SEI POSTAR MINHAS DUVIDAS?
Por favor, leia o tópico:
Primeiros Passos - Fórum AjudaMatemática.comviewtopic.php?f=9&t=5480Aproveite e leia também:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vanessa134 » Ter Out 18, 2011 23:19
por vanessa134 » Ter Out 18, 2011 23:19
Estou com dúvida justamente na justificativa.
Na questão 4 da atividade 2 MA001.
Para que (x,y)=p sabendo que x . y=p, no primeiro caso: x=1 e y=p e no segundo caso: x=p e y=1. Para que o par ordenado valha, o x ou o y precisam ser um número primo. Meu raciocínio está correto?
Todo número primo é divisível por 1 e por ele mesmo.
Vanessa
-
vanessa134
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Seg Out 17, 2011 00:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguem pode ajudar-me?
por carlos r m oliveira » Seg Out 05, 2009 11:35
- 1 Respostas
- 2552 Exibições
- Última mensagem por Neperiano

Dom Jul 03, 2011 21:05
Estatística
-
- Alguém pode me ajudar?
por apoliveirarj » Seg Jul 19, 2010 18:20
- 1 Respostas
- 3393 Exibições
- Última mensagem por Douglasm

Seg Jul 19, 2010 18:49
Matemática Financeira
-
- Alguém pode me ajudar?
por Andromeda » Seg Set 19, 2011 20:19
- 2 Respostas
- 2421 Exibições
- Última mensagem por Andromeda

Seg Set 19, 2011 21:13
Trigonometria
-
- lim x^2.sin(x/1), x=0. Alguém pode me ajudar?
por Arthur_Bulcao » Seg Abr 09, 2012 18:05
- 2 Respostas
- 2016 Exibições
- Última mensagem por fraol

Seg Abr 09, 2012 19:24
Cálculo: Limites, Derivadas e Integrais
-
- Alguém pode me ajudar?
por Cleyson007 » Qui Out 11, 2012 09:18
- 2 Respostas
- 4067 Exibições
- Última mensagem por Cleyson007

Qui Out 11, 2012 11:38
Pedidos de Materiais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



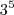 .
.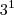 ,
, 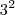 ,
, 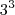 e
e 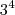 .
.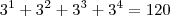 .
.



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.