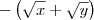por baril » Qua Set 28, 2011 22:32
por baril » Qua Set 28, 2011 22:32
De
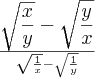
Em

Eu já tentei de tudo... até multiplicar em cima e baixo por
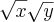
mas não consigo enxergar e chegar a

. Alguém caridoso pode fazer e explicar em detalhes para eu entender por favor? Desde já imensamente agradecido.
-
baril
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Set 28, 2011 22:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qui Set 29, 2011 10:09
por LuizAquino » Qui Set 29, 2011 10:09
Considerando
x e
y números positivos e não nulos, temos a expressão:
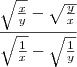
Usando a propriedade
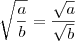
, ficamos com:
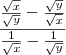
Efetuando a subtração entre as frações, temos que:

Efetuando a divisão entre as frações, resulta em:
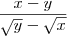
Multiplicando o numerador e o denominador por

, no final temos que:
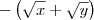
Reveja o seu gabarito, pois essa é a expressão correta.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- me ajude a simplificar por favor!!!!!!!
por barbosa » Dom Out 30, 2011 17:20
- 1 Respostas
- 1028 Exibições
- Última mensagem por DanielFerreira

Sex Nov 04, 2011 20:23
Álgebra Elementar
-
- [logaritmo] Ajude-me, por favor.
por Cleyson007 » Sáb Mai 17, 2008 23:20
- 4 Respostas
- 12836 Exibições
- Última mensagem por Neperiano

Qui Jun 19, 2008 16:34
Logaritmos
-
- [determinantes] Por favor me ajude!!!
por Cleyson007 » Dom Jul 13, 2008 09:11
- 3 Respostas
- 7187 Exibições
- Última mensagem por admin

Dom Jul 13, 2008 19:46
Matrizes e Determinantes
-
- [logaritmo] Ajude-me, por favor.
por Thayane Suzuki » Ter Ago 19, 2008 18:56
- 4 Respostas
- 6521 Exibições
- Última mensagem por admin

Sex Ago 22, 2008 00:38
Logaritmos
-
- me ajude urgente...por favor
por Leandrin » Qua Nov 10, 2010 14:06
- 1 Respostas
- 2154 Exibições
- Última mensagem por Neperiano

Sex Out 21, 2011 15:41
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
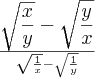

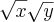 mas não consigo enxergar e chegar a
mas não consigo enxergar e chegar a  . Alguém caridoso pode fazer e explicar em detalhes para eu entender por favor? Desde já imensamente agradecido.
. Alguém caridoso pode fazer e explicar em detalhes para eu entender por favor? Desde já imensamente agradecido.
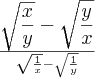

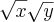 mas não consigo enxergar e chegar a
mas não consigo enxergar e chegar a  . Alguém caridoso pode fazer e explicar em detalhes para eu entender por favor? Desde já imensamente agradecido.
. Alguém caridoso pode fazer e explicar em detalhes para eu entender por favor? Desde já imensamente agradecido.
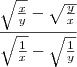
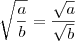 , ficamos com:
, ficamos com:

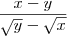
 , no final temos que:
, no final temos que: