"Um comerciante de veículos comercializa dois tipos de automóveis, um nacional e outro importado. Observa-se que, anualmente as vendas dos nacionais diminuem em 20% e as vendas dos importados aumenta 20%. Em 2004, 60% do total das vendas foram de carros nacionais e 40% de carros importados. Em 2006, o percentual de automóveis importados comercializados foi de 60%. certo ou errado?"
Eu coloquei como se o total de carros vendidos fosse 100, fica mais fácil de calcular, então venderam 60 nac e 40 impor. em 2004. Dos 60 nac. tirei 20% que deu 12, então subtrai dos 60, e em 2005 venderam 48. Desses 48 tirei 20% que deu 9,6, tirei dos 48 e ficou 38,4 em 2006. Ja achei estranho ai como vou ver 38 carros e 0,4 dele?
Aí dos importados fiz desse jeito: dos 100 venderam 40 tirei 20% que deu 8,e somei que ficou 48 carros em 2005, daí tirei 20% que deu 9,6 e somei, dando 57,6 carros importados em 2006...mas num ta certo como eu faço socorrooo...
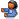
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.