Ambos os métodos resolvem qualquer tipo de sistema de equações lineares.
Não existe melhor método, o que existe é um método mais útil para cada situação.
O método da soma é útil quando você enxerga quais as operações que devem ser realizadas para cancelar uma varíavel.
Por exemplo aqui:
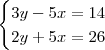
As equações estão quase pedindo para serem somadas. Fica tão simples que você consegue resolver de cabeça.
Se tentar resolver pelo método da substituição de cabeça fica bem mais complicado.
Mas nem sempre está tão evidente, as vezes você tem que multiplicar as duas equações para chegar a um fator comum que dê para cancelar, então alguns preferem ir direto para a substituição.
Vai de gosto mesmo, experimente e veja qual você se adapta melhor.
Mas aprenda bem o método da soma, pois quando você for resolver sistemas maiores com 3 equações e 3 incógnitas, por exemplo, você provavelmente usará uma técnica bem parecida com o método da soma que vai facilitar as coisas.


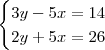



 , avisa que eu resolvo.
, avisa que eu resolvo.

