![\frac{1}{p} + \frac{1}{q} = \frac{1}{\sqrt[]{2010}} \frac{1}{p} + \frac{1}{q} = \frac{1}{\sqrt[]{2010}}](/latexrender/pictures/16c434558b78f2ff3ae8e62e1027459f.png) . Qual o valor mínimo do produto pq?
. Qual o valor mínimo do produto pq?oq consegui fazer foi somente o inicio e depois nao sei oq faço:
![\frac{p+q}{pq} = \frac{1}{\sqrt[]{2010}} \rightarrow p+q = \frac{pq}{\sqrt[]{2010}} \frac{p+q}{pq} = \frac{1}{\sqrt[]{2010}} \rightarrow p+q = \frac{pq}{\sqrt[]{2010}}](/latexrender/pictures/0da559bb010c5e1b7ac55e8304d37fda.png)
Infelismente nao sei oq fazer mais...
desde já grato.

![\frac{1}{p} + \frac{1}{q} = \frac{1}{\sqrt[]{2010}} \frac{1}{p} + \frac{1}{q} = \frac{1}{\sqrt[]{2010}}](/latexrender/pictures/16c434558b78f2ff3ae8e62e1027459f.png) . Qual o valor mínimo do produto pq?
. Qual o valor mínimo do produto pq?![\frac{p+q}{pq} = \frac{1}{\sqrt[]{2010}} \rightarrow p+q = \frac{pq}{\sqrt[]{2010}} \frac{p+q}{pq} = \frac{1}{\sqrt[]{2010}} \rightarrow p+q = \frac{pq}{\sqrt[]{2010}}](/latexrender/pictures/0da559bb010c5e1b7ac55e8304d37fda.png)

![\frac{1}{p}+\frac{1}{q}=\frac{1}{\sqrt[]{2010}} \frac{1}{p}+\frac{1}{q}=\frac{1}{\sqrt[]{2010}}](/latexrender/pictures/ff0b452167f0b238afbe83cc525d56ee.png)
![\frac{p+q}{pq}=\frac{1}{\sqrt[]{2010}} \frac{p+q}{pq}=\frac{1}{\sqrt[]{2010}}](/latexrender/pictures/96ff4eea56ba5117aeeda02f3618b376.png)
![\frac{p+q}{pq}=\frac{\sqrt[]{2010}}{2010} \frac{p+q}{pq}=\frac{\sqrt[]{2010}}{2010}](/latexrender/pictures/b3d4c370b9f2f07c13b0693d43fc7c2e.png)
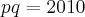

Guill escreveu:
Racionalizando:

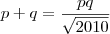
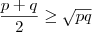 . Portanto,
. Portanto, 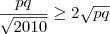 e segue que
e segue que 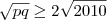 . Finalmente,
. Finalmente, 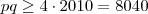 , e a resposta é que o valor mínimo de
, e a resposta é que o valor mínimo de 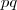 é 8040.
é 8040.

Guill escreveu:Racionalizando:
Joan escreveu:Amigo agradeço a boa vontade, mais no gabarito da prova tá a resposta como 8040. oq pode ta errado?
 , então não necessariamente a = c e b = d.
, então não necessariamente a = c e b = d.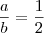 . Entretanto, note que
. Entretanto, note que 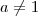 e
e 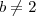 .
.

![\frac{p+q}{2}\geq\sqrt[2]{pq} \frac{p+q}{2}\geq\sqrt[2]{pq}](/latexrender/pictures/f431ac8ae5c2163d1397860bc2668184.png)



Fabricio dalla escreveu:eu n entendi o que Marcelo Fantine fez.ele pré supôs fazendo aquela comparaçao de que a media aritimetica e maior que media geometrica pra conseguir resolver a questão ?
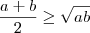 .
.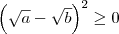 , para quaisquer a e b reais positivos.
, para quaisquer a e b reais positivos.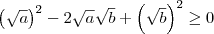
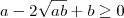
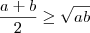

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)