Questão da UFU-MG

[Kelvin Brayan]

Sabendo-se que 302 400 = 64x27x25x7, pode-se concluir que o número de divisores de 302 400, que são múltiplos de 6, é igual a?

Eu já achei que 302 400 tem 168 divisores, mas como faço para descobrir o número de divisores múltiplos de 6 ?

[LuizAquino]

mas como faço para descobrir o número de divisores múltiplos de 6 ?

Para que um número seja múltiplo de 6 ele deve ser múltiplo de 2 e 3 ao mesmo tempo.

[Kelvin Brayan]

Tudo bem... mas qual é o procedimento que devo tomar para descobrir a quantidade de números divisores de 302 400 e múltiplos de 6 ? Como vou descobrir isso?

[LuizAquino]

Assim como foi feito no tópico [1], você pode determinar quantos são os divisores que não são múltiplos de 6. Em seguida, basta subtrair o total de divisores pelo total de divisores que não são múltiplos de 6.

Referência
[1] Questão UFV-MG - viewtopic.php?f=106&t=4513

[Kelvin Brayan]

Desculpem-me pela ignorância, mas será que alguém poderia resolver essa questão para mim ? Assim, eu poderia ver como se faz. Estou "enroscado" ainda somente nessa questão.


Obrigado !

[LuizAquino]

Sabemos que .

Como eu havia sugerido, vejamos quantos são os divisores que não são múltiplos de 6.

Para que o divisor não seja múltiplo de 6, os fatores e 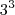não podem aparecer ao mesmo tempo.

Desse modo, queremos saber quantos são os divisores formados por:

• -- teremos (2+1)(1+1) = 6 divisores.
• -- teremos 6(2+1)(1+1) = 36 divisores. Note que no fator nós não podemos contabilizar a possibilidade , por esse motivo usamos 6 ao invés de (6+1).
• -- teremos 3(2+1)(1+1) = 18 divisores. Novamente, nós não podemos contabilizar a possibilidade , por esse motivo usamos 3 ao invés de (3+1).

Total de divisores que não são múltiplos de 6: 6 + 36 + 18 = 60.

Total de divisores: (6+1)(3+1)(2+1)(1+1) = 168.

Total de divisores que são múltiplos de 6: 168 - 60 = 108.

[Kelvin Brayan]

Ouu valeu mesmo ein!