 por guillcn » Seg Abr 11, 2011 12:22
por guillcn » Seg Abr 11, 2011 12:22
O enunciado pede o numero de algarismos do numro natural

eu gostaria de saber o modo para simplificar essa expressao porque senao terei que fazer inumeras multiplicaçoes.Obrigado.
-
guillcn
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Abr 05, 2011 16:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Seg Abr 11, 2011 14:29
por FilipeCaceres » Seg Abr 11, 2011 14:29
Veja que,
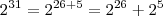
.
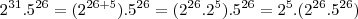
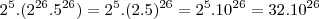
Como

(tem dois algarismos) e,
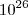
tem, 1 seguido de 26 algarismos zeros.
Agora, quando multiplica
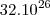
, dá um número natural, 32 seguindo de 26 zeros.
Logo, a soma será:
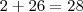
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por guillcn » Seg Abr 11, 2011 14:49
por guillcn » Seg Abr 11, 2011 14:49
valeu obrigadao.

-
guillcn
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Abr 05, 2011 16:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [potenciação] raiz cúbica com potenciação
por JKS » Qua Mar 06, 2013 17:41
- 2 Respostas
- 2290 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:43
Álgebra Linear
-
- [potenciação] módulo com potenciação
por JKS » Qua Mar 06, 2013 17:54
- 2 Respostas
- 1733 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:53
Equações
-
- POTENCIAÇÃO
por DANIELA » Sex Set 25, 2009 16:48
- 5 Respostas
- 3738 Exibições
- Última mensagem por DanielFerreira

Seg Set 28, 2009 10:20
Álgebra Elementar
-
- potenciação
por leandrofelip » Ter Fev 23, 2010 00:10
- 1 Respostas
- 2021 Exibições
- Última mensagem por Marcampucio

Ter Fev 23, 2010 12:56
Sistemas de Equações
-
- POTENCIACAO
por CaAtr » Ter Mar 09, 2010 20:23
- 3 Respostas
- 2290 Exibições
- Última mensagem por CaAtr

Ter Mar 09, 2010 22:17
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




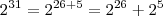 .
.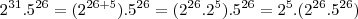
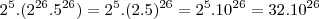
 (tem dois algarismos) e,
(tem dois algarismos) e,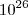 tem, 1 seguido de 26 algarismos zeros.
tem, 1 seguido de 26 algarismos zeros.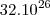 , dá um número natural, 32 seguindo de 26 zeros.
, dá um número natural, 32 seguindo de 26 zeros.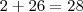




 .
.



