 por jose henrique » Sex Mar 25, 2011 14:20
por jose henrique » Sex Mar 25, 2011 14:20
![\sqrt[]{1-x} \sqrt[]{1-x} \Leftrightarrow \sqrt[]{(1-x)(1-x)}\Leftrightarrow \sqrt[]{{x}^{2}-2x+1} \sqrt[]{1-x} \sqrt[]{1-x} \Leftrightarrow \sqrt[]{(1-x)(1-x)}\Leftrightarrow \sqrt[]{{x}^{2}-2x+1}](/latexrender/pictures/1712a9e3268cd0dc7befce04c37ca756.png)
isso poderia ser feito, pois no meu livro o resultado é 1-x
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por profmatematica » Sex Mar 25, 2011 14:28
por profmatematica » Sex Mar 25, 2011 14:28
Eu nao sei add formulas aqui amigo mas vejamos resolvendo isso teremos raiz quadrada de (1-x) elevado ao quadrado dai corta o quadrado de (1-x) com o quadrado da raiz e sai da raiz apenas 1-x que e a resposta ok?
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Molina » Sex Mar 25, 2011 14:29
por Molina » Sex Mar 25, 2011 14:29
Boa tarde, José Henrique.
Poderia ser feito sim. O que você esqueceu, é que ao invés de fazer a distributiva, seria muito mais fácil deixar aquele termo ao quadrado:
![\sqrt[]{1-x} \sqrt[]{1-x} \Leftrightarrow \sqrt[]{(1-x)(1-x)}\Leftrightarrow \sqrt[]{(1-x)^2}=1-x \sqrt[]{1-x} \sqrt[]{1-x} \Leftrightarrow \sqrt[]{(1-x)(1-x)}\Leftrightarrow \sqrt[]{(1-x)^2}=1-x](/latexrender/pictures/9a3bc76cab4b3b2e7313bf6323606d1e.png)

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizAquino » Sex Mar 25, 2011 15:33
por LuizAquino » Sex Mar 25, 2011 15:33
Apenas lembrando que se
a é um número real qualquer, então
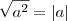
.
Sendo assim, temos que
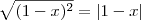
.
Se no exercício há a informação de que

, então aí sim poderíamos dizer que
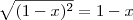
.
Editado pela última vez por
LuizAquino em Sáb Mar 26, 2011 11:33, em um total de 2 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jose henrique » Sáb Mar 26, 2011 10:58
por jose henrique » Sáb Mar 26, 2011 10:58
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- algebra l
por ehrefundini » Qui Mar 05, 2009 08:34
- 1 Respostas
- 7470 Exibições
- Última mensagem por Molina

Qui Mar 05, 2009 21:50
Álgebra
-
- algebra
por uspsilva » Sex Mar 13, 2009 13:03
- 1 Respostas
- 3219 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 15:22
Pedidos
-
- Algebra
por mattheusramos14 » Ter Ago 03, 2010 01:26
- 1 Respostas
- 2753 Exibições
- Última mensagem por MarceloFantini

Ter Ago 03, 2010 13:37
Álgebra Elementar
-
- ALGEBRA
por JOHNY » Sex Set 03, 2010 23:50
- 1 Respostas
- 2717 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:12
Álgebra Elementar
-
- álgebra
por Eliana Fidelis » Dom Out 24, 2010 13:52
- 1 Respostas
- 2662 Exibições
- Última mensagem por Adriano Tavares

Ter Mar 08, 2011 20:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{1-x} \sqrt[]{1-x} \Leftrightarrow \sqrt[]{(1-x)(1-x)}\Leftrightarrow \sqrt[]{{x}^{2}-2x+1} \sqrt[]{1-x} \sqrt[]{1-x} \Leftrightarrow \sqrt[]{(1-x)(1-x)}\Leftrightarrow \sqrt[]{{x}^{2}-2x+1}](/latexrender/pictures/1712a9e3268cd0dc7befce04c37ca756.png)

![\sqrt[]{1-x} \sqrt[]{1-x} \Leftrightarrow \sqrt[]{(1-x)(1-x)}\Leftrightarrow \sqrt[]{{x}^{2}-2x+1} \sqrt[]{1-x} \sqrt[]{1-x} \Leftrightarrow \sqrt[]{(1-x)(1-x)}\Leftrightarrow \sqrt[]{{x}^{2}-2x+1}](/latexrender/pictures/1712a9e3268cd0dc7befce04c37ca756.png)



![\sqrt[]{1-x} \sqrt[]{1-x} \Leftrightarrow \sqrt[]{(1-x)(1-x)}\Leftrightarrow \sqrt[]{(1-x)^2}=1-x \sqrt[]{1-x} \sqrt[]{1-x} \Leftrightarrow \sqrt[]{(1-x)(1-x)}\Leftrightarrow \sqrt[]{(1-x)^2}=1-x](/latexrender/pictures/9a3bc76cab4b3b2e7313bf6323606d1e.png)


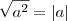 .
.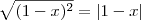 .
. , então aí sim poderíamos dizer que
, então aí sim poderíamos dizer que 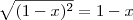 .
.

