Estou com dificuldades em resolver uma questão de trigonometria da UNEB, mais específicamente da concurso para o cfo.
Com sinceridade, não consigo imaginar uma maneira de resolver essa questão então decidi compartilhá-la com vocês.
Desde já, fico muito agradecido com a contribuição de cada um de vocês.
Abraço
40- Com relação à figura apresentada,
- o segmento OP representa a haste à qual é fixada a lâmina de borracha PQ, do limpador de parabrisa do vidro traseiro de um automóvel, segundo um ângulo constante
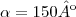
- a região sombreada apresenta a área A, varrida por PQ quando OP faz uma rotação em torno do centro O, de um ângulo
 no sentido anti-horário.
no sentido anti-horário.Sendo OP=PQ=x e
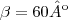 , pode-se afirmar que uma expressaõ válida para A em u.a é:
, pode-se afirmar que uma expressaõ válida para A em u.a é:





 , avisa que eu resolvo.
, avisa que eu resolvo.

