Ajuda equação de 2º grau
Olá, sou um aluno do 9° ano e recentemente o professor passou em minha prova a seguinte questão:
Papai noel gastou R$ 400,00 na compra de bolas para distribuir no dia de natal. Com um desconto de R$ 4,00 em cada uma, teria comprado 5 bolas a mais. Quantas bolas ele comprou?
Respondi em minha prova que a resposta era 20 bolas, pois 400/20 daria 20 reais cada bola, e 4 reais a menos em cada bola daria 16. 400 /16 é igual a 25, 25 - 5 é igual ao numero de bola que ele comprou.
A resposta dita pelo professor foi 16 pois segundo ele, 400/x - 4 = x + 5, e fazendo esta equação ele chegou aos resultados 16 e -25 dizendo que o resultado era 16.
Estou com dificuldade para entender a resposta dele pois 16bolas + 5 bolas daria 21 e sendo 16 bolas o preço de cada seria 25 reais, 25 - 4 reais daria 21 também, mas 21. 21 não da 400 reais.
Alguém poderia me ajudar a entender por favor?


 ele comprou
ele comprou 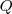 bolas gastando 400 reais, logo
bolas gastando 400 reais, logo 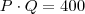 .
.  , compraria 5 bolas a mais, ou seja
, compraria 5 bolas a mais, ou seja  , porém continuaria gastando 400 reais, portanto temos
, porém continuaria gastando 400 reais, portanto temos  .
. , mas a primeira equação diz que
, mas a primeira equação diz que  , logo
, logo  .
.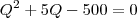 . As soluções são
. As soluções são  , que é descartada pois a quantidade é maior que zero e inteira, e
, que é descartada pois a quantidade é maior que zero e inteira, e  .
.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)