Mostre que para E = R^n e F = R^m temos:
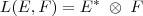
Onde L(E,F) é o espaço das aplicações lineares de E em F, E* é o dual de E e o produto entre E* e F é o produto tensorial entre os espaços.
Tentativa:
A tentativa consiste em fazer uma dupla inclusão entre os espaços, i.e., demonstrar que dado um elemento qualquer de L(E,F), este também se encontra em prodT(E*,F) e vice-versa. Se temos uma aplicação A de R^n em R^m, como afirmar que A é igual a um elemento de prodT(E*,F)? Alguém teria alguma dica?
Desde já agradeço


 . Não sei que resultados você tem ao seu dispor, mas se você notar que
. Não sei que resultados você tem ao seu dispor, mas se você notar que 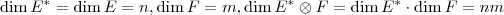 e
e 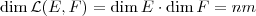 , portanto
, portanto 

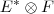 tal que:
tal que: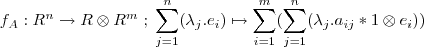
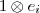 são base para
são base para 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)