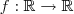 uma função tal que, dados dois Reais
uma função tal que, dados dois Reais  e
e  ,
, 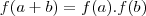 .
.Determine as soluções
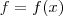 possíveis.
possíveis.Alguma idéia?

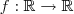 uma função tal que, dados dois Reais
uma função tal que, dados dois Reais  e
e  ,
, 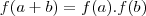 .
.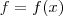 possíveis.
possíveis.

 ,
, 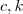 constantes reais.
constantes reais.


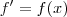 .
.


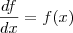 então a unicidade segue pelo teorema de existência e unicidade de equações diferenciais ordinárias.
então a unicidade segue pelo teorema de existência e unicidade de equações diferenciais ordinárias.

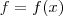 ? Apenas mostra que
? Apenas mostra que  é uma função da variável Real
é uma função da variável Real  .
.


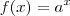 , com
, com 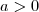 e
e 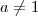 .
. tal que
tal que 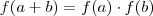 .
. é sempre positiva, pois:
é sempre positiva, pois: 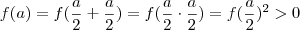 .
.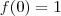 , pois:
, pois: 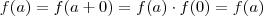 .
.  , pois:
, pois: 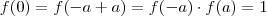 .
.
 . Você não pode afirmar que é maior que zero sempre (com apenas isso). Na segunda, deveria poder assumir que
. Você não pode afirmar que é maior que zero sempre (com apenas isso). Na segunda, deveria poder assumir que 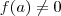 , o que não fez. Afirmar que
, o que não fez. Afirmar que 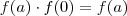 está tacitamente assumindo que
está tacitamente assumindo que  , que é o que quer provar. Para a terceira, está tudo OK, pois você partiu que
, que é o que quer provar. Para a terceira, está tudo OK, pois você partiu que  .
.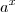 mas, se incluírmos a propriedade que
mas, se incluírmos a propriedade que 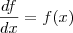 com
com  , então
, então 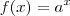 não é solução, e sim
não é solução, e sim  . Tanto que definimos e trabalhamos sempre com ela e chegamos nas outras a partir dela.
. Tanto que definimos e trabalhamos sempre com ela e chegamos nas outras a partir dela.

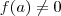 para valer 3 e, então valem, automaticamente, 1 e 2.
para valer 3 e, então valem, automaticamente, 1 e 2.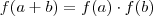 ? (
? ( 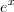 não é um caso particular de
não é um caso particular de 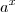 ? )
? ) em
em 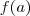 é um
é um  do domínio e o
do domínio e o  de
de 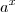 é uma base - pode ficar um pouco confuso eu ter usado o mesmo símbolo para duas coisas diferentes.
é uma base - pode ficar um pouco confuso eu ter usado o mesmo símbolo para duas coisas diferentes.
MarceloFantini escreveu:Ele quer determinar todas as funções que satisfaçam esta propriedade?
MarceloFantini escreveu:Você quer encontrar funções tal que a imagem da soma seja produto das imagens, e tenho quase certeza de que não é suficiente para caracterizar a função exponencial.



 ser solução única ( no caso de classificar funções: exponencial, harmonica, polinomial, etc...) é uma caracteristica particular da equação. Não que a exponencial
ser solução única ( no caso de classificar funções: exponencial, harmonica, polinomial, etc...) é uma caracteristica particular da equação. Não que a exponencial  é uma solução particular. Sei que para isto deveríamos acrescentar informações ao problema, como valores iniciais.
é uma solução particular. Sei que para isto deveríamos acrescentar informações ao problema, como valores iniciais.

fraol escreveu:Ok. Você está certo, aliás devemos assumir quepara valer 3 e, então valem, automaticamente, 1 e 2.
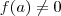 não é uma condição, é uma propriedade oriunda da propriedade geral dada no início (
não é uma condição, é uma propriedade oriunda da propriedade geral dada no início ( 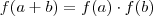 ). Isto ocorre pois se
). Isto ocorre pois se  for nula para algum
for nula para algum 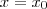 então ela será nula para todo o
então ela será nula para todo o  .
.
 Eu já sabia disso.
Eu já sabia disso.





?Como já sabemos que é verdadeira, mesmo que não saibamos justificar ...


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.