 por Talitafreire » Qui Jul 09, 2009 17:29
por Talitafreire » Qui Jul 09, 2009 17:29
Olá gente. Sou novata e entrei aqui pq tenho uma dúvida em uma questão q caiu numa prova de cálculo q fiz.
Bom, a questão pede para esboçar o gráfico da seguinte função:

Já consegui encontrar os pontos críticos, concavidades, os intervalos onde a função é crescente e decrescente, o limite quando tende a zero, mas estou com muita dificuldade para encontrar as assíntotas dessa função (se é q elas existem), oq faz com q meu gráfico não saia. :/. Quem puder, ajude-me ok? Obrigada desde já.
-
Talitafreire
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jul 09, 2009 17:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química (Bacharelado)
- Andamento: cursando
 por Marcampucio » Qui Jul 09, 2009 17:59
por Marcampucio » Qui Jul 09, 2009 17:59
Veja Talita,
o domínio da função é todo o campo Real, portanto ela é contínua e não tem assíntotas verticais.

anlogamente
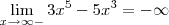
a função não tem assíntotas horizontais também.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Talitafreire » Qui Jul 09, 2009 18:03
por Talitafreire » Qui Jul 09, 2009 18:03
Marcampucio escreveu:Veja Talita,
o domínio da função é todo o campo Real, portanto ela é contínua e não tem assíntotas verticais.

anlogamente
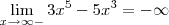
a função não tem assíntotas horizontais também.
Muito obrigada pela resposta ^^ \o/ mesmo mesmo Tentarei montar esse gráfico entao. Até.
-
Talitafreire
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jul 09, 2009 17:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química (Bacharelado)
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Grafico de limites e assintotas
por Bruhh » Qui Abr 15, 2010 15:43
- 3 Respostas
- 5297 Exibições
- Última mensagem por Marcampucio

Sex Abr 16, 2010 21:07
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Iniciação (Gráfico - assíntotas)
 por ViniciusAlmeida » Seg Fev 09, 2015 12:35
por ViniciusAlmeida » Seg Fev 09, 2015 12:35
- 0 Respostas
- 941 Exibições
- Última mensagem por ViniciusAlmeida

Seg Fev 09, 2015 12:35
Cálculo: Limites, Derivadas e Integrais
-
- Encontrando as raízes!
por gfdbruno » Qui Ago 25, 2011 10:36
- 1 Respostas
- 2530 Exibições
- Última mensagem por gfdbruno

Qui Ago 25, 2011 12:53
Polinômios
-
- assíntotas
 por pseytow » Qua Jul 02, 2008 13:11
por pseytow » Qua Jul 02, 2008 13:11
- 2 Respostas
- 5482 Exibições
- Última mensagem por admin

Sex Jul 04, 2008 05:39
Cálculo: Limites, Derivadas e Integrais
-
- assíntotas
por aquis » Qua Set 10, 2014 11:49
- 0 Respostas
- 1645 Exibições
- Última mensagem por aquis

Qua Set 10, 2014 11:49
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
