Sou iniciante em calculo e me deparei com a seguinte questão (cos x.senx )/(tg x), não sei como aplicar as duas fórmulas ao mesmo tempo.
Obrigada pela atenção!
por karinak » Sáb Jun 16, 2012 02:08
por Jhonata » Sáb Jun 16, 2012 10:58
karinak escreveu:Sou iniciante em calculo e me deparei com a seguinte questão (cos x.senx )/(tg x), não sei como aplicar as duas fórmulas ao mesmo tempo.
Obrigada pela atenção!
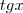e a reescreva como: 
.
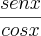. Podemos fazer um cancelamento e ficaremos apenas com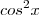 
.
* 
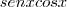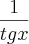e aplicar a regra do produto fazendo f(x)=senxcosx e g(x)=1/tgx, mas nessa aplicação você aplicaria várias vezes a regra dentro de regra, o que seria muito trabalhoso.
por karinak » Sáb Jun 16, 2012 12:43
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)