 por Eduardooitavo » Sáb Jun 09, 2012 18:06
por Eduardooitavo » Sáb Jun 09, 2012 18:06
Nao estou conseguindo calcular os intervalos desta funcao x2/x2 - 4, ja achei a derivada da funcao.
obs: x2 = x ao quadrado
A derivada eh -8x/ [(x+2)(x-2)] ao quadrado, depois disso nao sei mais o que fazer. Preciso acha os pontos maximos e minimos.
Se alguem conseguir agradeco.
-
Eduardooitavo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Jun 09, 2012 18:00
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Sáb Jun 09, 2012 19:32
por MarceloFantini » Sáb Jun 09, 2012 19:32
Você tem a função
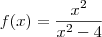
, logo
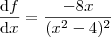
.
Para encontrar os pontos de máximo e mínimo devemos fazer
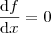
, portanto
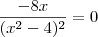
. De cara já sabemos que

e
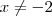
devido ao denominador. Quais são as outras possíveis raízes?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Intervalos de crescimento e decrescimento da função
por valeuleo » Ter Jun 21, 2011 21:50
- 3 Respostas
- 3454 Exibições
- Última mensagem por LuizAquino

Ter Jun 21, 2011 22:44
Cálculo: Limites, Derivadas e Integrais
-
- crescimento e decrescimento da função
por Ana Maria da Silva » Qua Out 02, 2013 10:18
- 1 Respostas
- 1166 Exibições
- Última mensagem por Bravim

Qui Out 03, 2013 05:32
Cálculo: Limites, Derivadas e Integrais
-
- crescimento e decrescimento
por joandro » Dom Abr 13, 2014 11:30
- 1 Respostas
- 1472 Exibições
- Última mensagem por alienante

Ter Abr 29, 2014 17:27
Cálculo: Limites, Derivadas e Integrais
-
- Intervalo de crescimento e decrescimento
por valeuleo » Qui Jun 23, 2011 12:02
- 4 Respostas
- 2853 Exibições
- Última mensagem por LuizAquino

Sáb Jun 25, 2011 16:50
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] crescimento e decrescimento
por fabriel » Ter Set 25, 2012 02:57
- 2 Respostas
- 1931 Exibições
- Última mensagem por fabriel

Ter Set 25, 2012 12:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


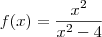 , logo
, logo 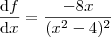 .
.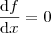 , portanto
, portanto 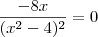 . De cara já sabemos que
. De cara já sabemos que  e
e 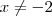 devido ao denominador. Quais são as outras possíveis raízes?
devido ao denominador. Quais são as outras possíveis raízes?
