UM CASAL FOI COMPRAR UMA GELADEIRA EM X PRESTAÇÕES IGUAIS. COMPRANDO A GELADEIRA COM TRÊS PRESTAÇÕES A MENOS, CADA PRESTAÇÃO AUMENTARIA R$30,00, E SE COMPRASSE COM 6 PRESTAÇÕES A MENOS, CADA PRESTAÇÃO AUMENTARIA R$75,00. O CASAL DECIDIU ENTÃO COMPRAR A GELADEIRA PAGANDO EM X PRESTAÇÕES. NESSAS CONDIÇÕES O VALOR DE X É:
a) 30
b) 24
c) 18
d) 15
e) 12
tentei inicialmente pensar em igualar a incógnita
x-3=p+30
x-6= p+75
multiplicando a 1ª equação por -2 e transformando em sistema teriamos:
-2x+6=-2p-60
x-6= p+75
igual a -x=-p+15 então substituindo x=p-15 em
x-6=p+75 temos p-15=p+75 que é igual a 2p=90 temos que p=45 não seiiiiii


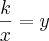 ===========>
===========> 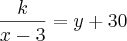
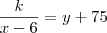
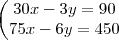
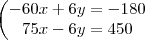


 .
.



