Antes de mais a expressão que apresentas traduz a definição de derivada num dado ponto. Neste caso x=0.
É verdade que quando se tenta comutar a expressão com os devidos valores, nos deparamos com a situação de

.
Rapidamente paramos para pensar e reconhecemos uma daquelas funções elementares de cujo gráfico todos devemos de memorizar. Neste caso temos
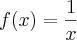
.
Através de um simulador gráfico podemos vizualizar que esta função é continua em todos os pontos exeto em x=0. Logo se não é continua, não é diferenciavel. Não é continua porque os limites laterais quando
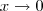
não são iguais.
Para ser diferenciavel é necessário que seja continua e que o declive da reta tangente(derivada) seja igual, quer
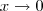
pela esquerda, quer
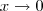
pela direita.
Logo concluímos que está função não tem derivada em x=0.
Pela definição de derivada:
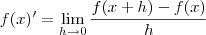
Obtemos:
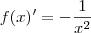
cujo o dominio é R\{0}.






 .
.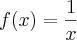 .
.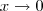 não são iguais.
não são iguais.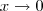 pela esquerda, quer
pela esquerda, quer 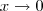 pela direita.
pela direita.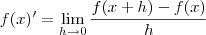
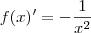 cujo o dominio é R\{0}.
cujo o dominio é R\{0}.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)