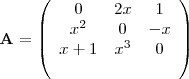
seja:
a) simétrica b) anti-simétrica
Apliquei a definição de matriz simétrica =
 e igualdade de matrizes veriquei que não são simétricas pois Aij
e igualdade de matrizes veriquei que não são simétricas pois Aij Bji. E o unico valor para que a equação seja simétrica é o zero.
Bji. E o unico valor para que a equação seja simétrica é o zero.Apliquei a definição de matriz anti-simétrica=
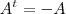 fica claro pela definição que não são simétrica tudo isso antes de achar o valor par x que sendo zero passa a ser simétrica na pergunta A e anti-simétrica na pergunta B.
fica claro pela definição que não são simétrica tudo isso antes de achar o valor par x que sendo zero passa a ser simétrica na pergunta A e anti-simétrica na pergunta B.Gostaria agradeço desde já o apoio de vocês da equipe.
Jesus abençoe a todos. Amém!
Muito obrigado


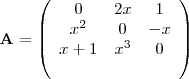
 . E o unico valor para que a equação seja simétrica é o zero.
. E o unico valor para que a equação seja simétrica é o zero.


 , avisa que eu resolvo.
, avisa que eu resolvo.

