 por maramollica16 » Qui Fev 16, 2012 12:31
por maramollica16 » Qui Fev 16, 2012 12:31
Boa tarde
Estou estudando sozinha para um Concurso Público, tenho muitas duvidas por que estou no Ensino Médio ainda.
Minha Dúvida é como resolver essa POTENCIA:
2 3
3 e 4 , é uma operação simples mas estou com dificuldade.
RAIZ QUADRADA:
do número 16 e 25 ?
Obrigada mesmo !!!!
-
maramollica16
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Fev 16, 2012 12:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qui Fev 16, 2012 16:37
por MarceloFantini » Qui Fev 16, 2012 16:37
Boa tarde Mara. Não é possível entender que tipo de potências você quer dizer. Para escrever em latex, use o código como exemplo:
- Código: Selecionar todos
[tex]2^{3}[/tex]
imprime na tela
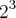
. Analogamente para radiciação, temos
- Código: Selecionar todos
[tex]\sqrt{16}[/tex]
que imprime

, e em caso de índices maiores use
- Código: Selecionar todos
[tex]\sqrt[n]{16}[/tex]
que imprime
![\sqrt[n]{16} \sqrt[n]{16}](/latexrender/pictures/70ceda6f256b50e9bbb712d9563dccaa.png)
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite com raiz enésima - como calcular?
por Brunorp » Ter Mar 24, 2015 08:56
- 1 Respostas
- 8822 Exibições
- Última mensagem por adauto martins

Qui Mar 26, 2015 16:17
Cálculo: Limites, Derivadas e Integrais
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7466 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Raiz quadrada
por j1a4l0 » Qui Abr 22, 2010 18:05
- 5 Respostas
- 6008 Exibições
- Última mensagem por Neperiano

Sex Abr 23, 2010 09:35
Funções
-
- raiz quadrada
por jose henrique » Seg Ago 16, 2010 16:54
- 1 Respostas
- 2353 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:03
Álgebra Elementar
-
- [Raiz quadrada de 13] Na mão
por Mickdark » Dom Abr 08, 2012 20:00
- 4 Respostas
- 17651 Exibições
- Última mensagem por Mickdark

Qui Abr 12, 2012 09:56
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


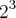 . Analogamente para radiciação, temos
. Analogamente para radiciação, temos , e em caso de índices maiores use
, e em caso de índices maiores use![\sqrt[n]{16} \sqrt[n]{16}](/latexrender/pictures/70ceda6f256b50e9bbb712d9563dccaa.png) .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.