Galerinha inteligentee, eu queriia tirar uma duvida:
estava estudando e no livro há uma questão assim
Elimine o módulo:
1. |-a| , se a > 0 a resposta é a
2. |-a| a resposta é -a, se a>=0 e a, se a < 0
eu não estou conseguindo entender as duas respostas diferentes. se puderem me explicar.


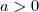 então
então 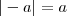 é um número positivo.
é um número positivo.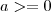 então
então 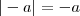 é um número negativo e contradiz a definição.
é um número negativo e contradiz a definição.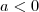 então
então 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)