 por luiz_melodia » Sáb Dez 24, 2011 12:17
por luiz_melodia » Sáb Dez 24, 2011 12:17
![lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1} lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1}](/latexrender/pictures/ab1c4017cabee49e1c1aa6b231d102ca.png)
, fazer sem L'HOSPITAL apenas com definicao e as prpriedades de limite
-
luiz_melodia
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Dez 24, 2011 10:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: comp
- Andamento: cursando
 por LuizAquino » Sáb Dez 24, 2011 18:13
por LuizAquino » Sáb Dez 24, 2011 18:13
luiz_melodia escreveu:![\lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1} \lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1}](/latexrender/pictures/31e8915442b3e3ce915de49cca13291e.png)
, fazer sem L'HOSPITAL apenas com definicao e as prpriedades de limite
DicaComece fazendo a substituição
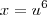
.
![\lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1} = \lim_{u \to 1}\frac{u^2 - 1}{u^3 - 1} \lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1} = \lim_{u \to 1}\frac{u^2 - 1}{u^3 - 1}](/latexrender/pictures/1f8668b59a01e504a7658d25b8f650be.png)
Agora use produtos notáveis e tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1} lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1}](/latexrender/pictures/ab1c4017cabee49e1c1aa6b231d102ca.png) , fazer sem L'HOSPITAL apenas com definicao e as prpriedades de limite
, fazer sem L'HOSPITAL apenas com definicao e as prpriedades de limite

![lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1} lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1}](/latexrender/pictures/ab1c4017cabee49e1c1aa6b231d102ca.png) , fazer sem L'HOSPITAL apenas com definicao e as prpriedades de limite
, fazer sem L'HOSPITAL apenas com definicao e as prpriedades de limite
, fazer sem L'HOSPITAL apenas com definicao e as prpriedades de limite
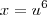 .
.![\lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1} = \lim_{u \to 1}\frac{u^2 - 1}{u^3 - 1} \lim_{x \to 1}\frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1} = \lim_{u \to 1}\frac{u^2 - 1}{u^3 - 1}](/latexrender/pictures/1f8668b59a01e504a7658d25b8f650be.png)
