Olá pessoal,
Acredito que a resposta é
- Código: Selecionar todos
x = 50123 e y = 49876, em que x - y = 247
.
Como cheguei a esse resultado:
Admitimos que x e y não podem começar com o algarismo 0, pois senão algum deles teria apenas 4 algarismos (ok, qualquer cego vê isso!!!).
Assumimos que desconhecemos o primeiro algarismo tanto de x quanto de y (na realidade não sabemos mesmo...). Vamos descobrir a partir do segundo em diante.
Bom, como x > y e estamos interessados na menor diferença entre os dois, devemos escolher os algarismos seguintes de maneira que 'forcemos' x a ser o menor valor possível e y a ser o maior valor possível. Tendo isso em mente, o segundo algarismo de x deve ser 0 (já que não pode ser o primeiro!), o terceiro 1, o quarto 2 e o quinto 3 e o segundo algarismo de y deve ser 9, o terceiro 8, o quarto 7 e o quinto 6. Logo
x = ? 0123 e y = ? 9876 obviamente para a diferença não ser um valor negativo x = 50123 e y = 49876!
Porém, acho que tem um jeito mais fácil de raciocinar sobre este problema, que consiste tentar encontrar o menor valor para x e o maior valor para y simultaneamente, de maneira que x > y e não se repita nenhum algarismo entre os dois números.
Dessa forma
O primeiro algarismo de x deve ser 5, pois se fosse 6, 7, 8 ou 9 não seria o menor possível e se fosse 4, 3, 2 ou 1 impediria y de ter o valor 4.
O primeiro algarismo de y deve ser 4, pois se fosse 0, 1, 2 ou 3 não seria o menor possível e se fosse 5, 6, 7, 8 ou 9 impediria x de ter o valor 5.
Essas duas premissas podem ser pensadas intuitivamente, principalmente na hora da prova, mas podem ser comprovadas por permutação de x e y (eu acho!):
x y x y x y ....
9 1 9 2 9 3 ....
8 1 8 2 8 3 ....
7 1 7 2 7 3 ....
... .... .....
De maneira semelhante ao raciocínio anterior, os algarismos seguintes a x seriam 0, 1, 2 e 3 e os seguintes a y seriam 9, 8, 7 e 6.
Espero ter ajudado!
Abraços


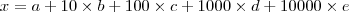
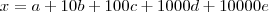
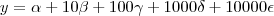
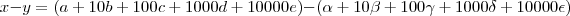
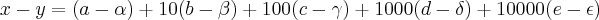
 e
e  são iguais a zero... pois os numeros tem só 3 algarismos. E isso nos leva a perceber que
são iguais a zero... pois os numeros tem só 3 algarismos. E isso nos leva a perceber que  ... o mesmo pra 'e' e 'epsilon'
... o mesmo pra 'e' e 'epsilon'





