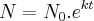 em que N é o número de bactérias, t é o tempo em horas e K é a taxa de cresciemnto.
em que N é o número de bactérias, t é o tempo em horas e K é a taxa de cresciemnto.Eu realizei de tal forma:
Considerando o primeiro instante, onde N=1000, t=0, obtive que

Com t=
 ,
, 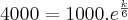
![4000= \sqrt[6]{{e}^{k}} 4000= \sqrt[6]{{e}^{k}}](/latexrender/pictures/2a14f513540a1c589cc6b626c15c6696.png)

Então, em t=1
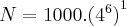
N = 4,096.
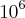
Está correto?

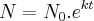 em que N é o número de bactérias, t é o tempo em horas e K é a taxa de cresciemnto.
em que N é o número de bactérias, t é o tempo em horas e K é a taxa de cresciemnto.
 ,
, 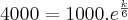
![4000= \sqrt[6]{{e}^{k}} 4000= \sqrt[6]{{e}^{k}}](/latexrender/pictures/2a14f513540a1c589cc6b626c15c6696.png)

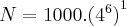


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes