 por kryzay » Qua Jul 27, 2011 09:20
por kryzay » Qua Jul 27, 2011 09:20
Fala galera, como vai?
Estou com dúvida em resolver esse exercício. Eu não entendi a explicação de como proceder.
Será que alguém pode ajudar. Estou a um bom tempo matutando a cabeça.

Eu coloquei na imagem todas as questões, mas eu quero saber como faz apenas
UMA.
Se alguém entender e souber me explicar como devo fazer ficarei muito agradecido.
-
kryzay
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Jul 25, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Guill » Qua Jul 27, 2011 11:25
por Guill » Qua Jul 27, 2011 11:25

Isso é um polinômio. Ele pode ser escrito assim:

As raízes desse polinômio são a,b...,y,z.
Se você multiplicar esse polinômio, fica claro que:
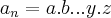
An é o produto de todas as raízes da equação. Considere que

é uma raíz da equação. Isso quer dizer que o termo independente An tem

como seu produto:
An = a.b.

...y.z
Isso prova que

divide An.
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por kryzay » Qua Jul 27, 2011 11:49
por kryzay » Qua Jul 27, 2011 11:49
Fala Guill,
Eu entendi sua explicação.
Exceto por:
"Isso é um polinômio. Ele pode ser escrito assim:
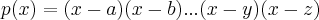
As raízes desse polinômio são a,b...,y,z."Queria saber como eu coloco um polinônio dessa forma.
Se for possível tenta dar um exemplo com uma equação do 3º grau, como a letra A por exemplo.
-
kryzay
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Jul 25, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Guill » Qua Jul 27, 2011 12:16
por Guill » Qua Jul 27, 2011 12:16
Qualquer polinômio pode ser escrito dessa forma. Por exemplo:
x² - 4x + 3 = 0
Observa-se claramente que as raízes dessa equação são 3 e 1. Para escrever como um polinômio:
(x - 3)(x - 1) = 0
Raízes = {1;3}
Substitua uma raíz qualquer no polinômio:
(x - 3)(x - 1) = 0
(3 - 3)(3 - 1) = 0
0.2 = 0
0 = 0
(x - 3)(x - 1) = 0
(1 - 3)(1 - 1) = 0
-2.0 = 0
0 = 0
As raízes zeraram o polinômio. Essa forma de escrever é a forma fatorada desse polinômio. Para escrever ele assim, deve-ter as raízes dele:
Se uma equação qualquer tem raízes 1, -2 e 3.
Então, basta inverter o sinal:
(x - 1)(x + 2)(x - 3) = 0
Se multiplicar termo a termo, terá a equação:
(x² + x - 2)(x - 3) = 0
x³ - 2x² - 5x + 6 = 0
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por kryzay » Qua Jul 27, 2011 12:22
por kryzay » Qua Jul 27, 2011 12:22
Entendi Guill, eu até tinha feito no caderno aqui.

No entanto, minha dúvida eh assim:
Temos essa equação, por exemplo:
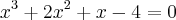
Como você iria encontrar as raízes?
Obg.
-
kryzay
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Jul 25, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Guill » Qua Jul 27, 2011 12:43
por Guill » Qua Jul 27, 2011 12:43
Não existe uma fórmula geral para isso. E eu não sei muito arespeito dessas equações porque eu estou no 2º ano do ensino médio. Mas eu conheço uma técnica que é assim:
x³ + 2x² + x - 4 = 0
1.x³ + 2.x² + 1.x - 4 = 0
Ache os divisores de a e d (levando em consideração que a equação é ax³ + bx² + cx + d = 0):
D = {-1;1;2;-2;-4;4}
Substituia cada uma na equação:
x³ + 2x² + x - 4 = 0
(-1)³ + 2(-1)² + (-1) - 4 = 0
-1 + 2 - 1 - 4 = 0
-4 = 0 (-1 não é raíz)
(1)³ + 2(1)² + 1 - 4 = 0
-3 + 3 = 0
0 = 0 (1 é raíz)
(-2)³ + 2(-2)² + (-2) - 4 = 0
-8 + 8 - 6 = 0
-6 = 0 (-2 não é raíz)
(2)³ + 2(2)² + (2) - 4 = 0
8 + 8 - 2 = 0
14 = 0 (2 não é raíz)
(-4)³ + 2(-4)² + (-4) - 4 = 0
-64 + 24 = 0 (-4 não é raíz)
(4)³ + 2(4)² + (4) - 4 = 0
64 + 32 = 0 (4 não é raíz)
1 é a única raíz INTEIRA dessa equação. Esse método só serve para encontrar as raízes inteiras.
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por kryzay » Seg Ago 01, 2011 10:08
por kryzay » Seg Ago 01, 2011 10:08
Fala Guill,
Desculpe a demora para responder, é que esse assunto me deu muito a que pesquisar.
Com o exercício eu aprendi:
* Nova forma de um polinômio (Guill)
* Encontrar Raizes inteiras (Guill)
E procurando eu encontrei o dispositivo de Briott-Ruffini.
Com ele eu posso dividir qualquer polinômio por um monômio do tipo x-a.
Queria te agradecer Guill, você me ajudou muito aqui.
Espero que o exercicio possa ajudar outras pessoas também.
-
kryzay
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Jul 25, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por LuizAquino » Seg Ago 01, 2011 12:14
por LuizAquino » Seg Ago 01, 2011 12:14
Guill escreveu:
Isso é um polinômio. Ele pode ser escrito assim:

Uma pequena correção. Faltou colocar o termo
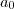
multiplicando toda a forma fatorada.
Isto é, se

,
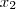
, ...,
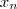
são as raízes de p(x), então a sua forma fatorada será:

Exemplo:
A forma fatorada de
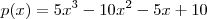
é:
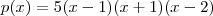
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Buda » Sáb Out 29, 2011 23:04
por Buda » Sáb Out 29, 2011 23:04
Esse assunto nao tem muitas formulas especificas.Mais com muita pratica fica um assunto muito facil.
A eq. x^3 + 2x^2 +x - 4 =0
É uma eq. do 3° grau. para essa funçao vc vai fazer o seguinte.
pegue o valor de ''d'' da eq. y = ax^3 + bx^2 + cx + d . Neste exercicio o '''d'' = 4
e pegue seus valores multiplos. no exemplo -+ 1 , -+2, -+4. E substitua na funçao y todos os valores, um de cada por vez. E o que der y(do valor) =0 essa é sua raiz
Nota: se o valor ''a'' da funçao for diferente de 1, por exemplo 4. Neste exemplo vc vai ter que pegar valores dividos por 4 tambem.
-+1, -+2, -+4, -+1/4, -+ 2/4 que é igual a -+1/2, e -+4/4 que ja foi feito anteriormente na primeira tentativa.Para ''a'' = 4 eu nao tentei neste exato exemplo, portanto eu nao sei se vai funcionar.
Obs: Mais este metodo funciona em maior parte das vezes. So tem problemas quando ouver raizes complexas.Que raramente cai no vestibular, ou ensino medio.Este metodo pode ser usado tanto em equaçoes do 2° como 3° e assim vai.
Continuando o exercicio. substituindo os valores vc vai axar uma das raizes x= 1 . portanto y(1)=0
entao voce pode dividir a funçao x^3 + 2x^2 +x - 4 por x-1. Onde a x-1=0 x=1 é a raiz.
fazendo a divisao ficara.
quociente = x^2 + 3x + 4
resto = 0
A funçao x^2 + 3x + 4 nao tem raiz real. Portanto a funçao x^3 + 2x^2 +x - 4 =0 tem apenas uma raiz real x=1.
para saber se a funçao tem raiz dupla, uma apenas ou nenhuma. É so usar bascara,a parte do Delta = (b² -4ac)^0,5 , se der um valor positivo tem 2 raizes, se for igual a zero 1 raiz, e negativo nao tem raiz.
No exercicio 17. Voce pode usar este metodo que achara todas as raizes.
-
Buda
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Out 24, 2011 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Guidorizzi
por manuoliveira » Qua Set 12, 2012 21:09
- 1 Respostas
- 5802 Exibições
- Última mensagem por MarceloFantini

Qua Set 12, 2012 22:04
Cálculo
-
- Diferenciabilidade [Guidorizzi]
por PScotth » Sáb Jun 23, 2018 09:57
- 0 Respostas
- 2656 Exibições
- Última mensagem por PScotth

Sáb Jun 23, 2018 09:57
Cálculo: Limites, Derivadas e Integrais
-
- Exercício de derivadas - Guidorizzi
por -civil- » Qui Mai 19, 2011 10:26
- 2 Respostas
- 3999 Exibições
- Última mensagem por -civil-

Seg Mai 23, 2011 00:24
Cálculo: Limites, Derivadas e Integrais
-
- Exercicio de 'Prove que...' guidorizzi.
por TheoFerraz » Ter Mai 24, 2011 18:22
- 1 Respostas
- 1929 Exibições
- Última mensagem por LuizAquino

Ter Mai 24, 2011 20:47
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Cálculo de Áreas - Guidorizzi
por Lennon » Sáb Jun 08, 2013 02:24
- 2 Respostas
- 2831 Exibições
- Última mensagem por Lennon

Dom Jun 09, 2013 22:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





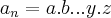
 é uma raíz da equação. Isso quer dizer que o termo independente An tem
é uma raíz da equação. Isso quer dizer que o termo independente An tem 
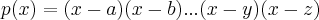
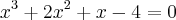
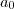 multiplicando toda a forma fatorada.
multiplicando toda a forma fatorada. ,
, 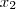 , ...,
, ..., 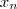 são as raízes de p(x), então a sua forma fatorada será:
são as raízes de p(x), então a sua forma fatorada será:
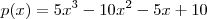 é:
é: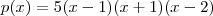




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.